《2025年假期冲冠黑龙江教育出版社八年级数学》

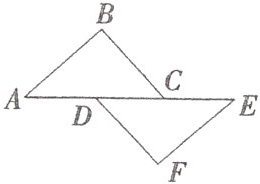
1. 如图,点 A,D,C,E 在同一条直线上,$AB// EF,AB= EF,∠B= ∠F,AE= 12,AC= 8$,则 CD 的长为 ( )


A.5.5
B.4
C.4.5
D.3

答案： B

2. 如图,已知$AB= AD,∠BAE= ∠DAC$,要使$△ABC\cong △ADE$. 若以“SAS”为依据,则补充的条件是____.

答案： $AC = AE$

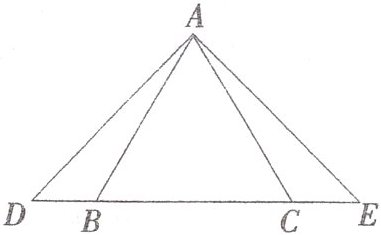
3. 如图,$△ABC$是等边三角形,D,E 在直线 BC 上,$DB= EC$. 求证:$∠D= ∠E.$

答案： 证明：$\because \triangle ABC$是等边三角形，$\therefore AB = AC$，$\angle ABC = \angle ACB$，$\therefore \angle ABD = \angle ACE$，
在$\triangle ADB$和$\triangle AEC$中，
$\left\{\begin{array}{l} AB = AC \\ \angle ABD = \angle ACE \\ DB = EC \end{array}\right.$
$\therefore \triangle ADB \cong \triangle AEC(SAS)$，$\therefore \angle D = \angle E$。

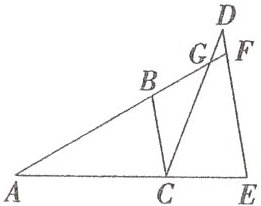
4. 如图,点 C 在线段 AE 上,$BC// DE,AC= DE,BC= CE$. 延长 AB 分别交 CD,ED 于点 G,F.
(1)求证:$AB= CD;$
(2)若$∠ACB= 65^{\circ },∠DCE= 75^{\circ }$,求$∠FGC$的度数.

答案： 解：
(1) 证明：$\because BC // DE$，$\therefore \angle ACB = \angle CED$。在$\triangle ABC$与$\triangle DCE$中，
$\left\{\begin{array}{l} AC = DE \\ \angle ACB = \angle DEC \\ BC = CE \end{array}\right.$，$\therefore \triangle ABC \cong \triangle DCE(SAS)$，
$\therefore AB = CD$。
(2) 解：$\because \triangle ABC \cong \triangle DCE$，$\therefore \angle A = \angle D$，$\angle ABC = \angle DCE = 75^{\circ}$。$\because \angle ACB = 65^{\circ}$，$\therefore \angle A = \angle D = 180^{\circ} - 75^{\circ} - 65^{\circ} = 40^{\circ}$，
$\therefore \angle FBC = \angle A + \angle ACB = 40^{\circ} + 65^{\circ} = 105^{\circ}$。$\because BC // DE$，$\therefore \angle DFB = \angle FBC = 105^{\circ}$。$\therefore \angle FGC = \angle D + \angle DFB = 40^{\circ} + 105^{\circ} = 145^{\circ}$。

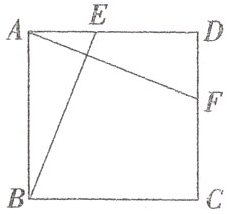
5. 如图,在正方形 ABCD 中,E,F 分别是边 AD,DC 上的点,且$AF⊥BE$. 求证:$AF= BE.$

答案： 证明：$\because$四边形$ABCD$是正方形，$\therefore AB = DA$，$\angle D = \angle EAB = 90^{\circ}$。$\therefore \angle FAD + \angle BAF = 90^{\circ}$。$\because BE \perp AF$，
$\therefore \angle BAF + \angle ABE = 90^{\circ}$。$\therefore \angle ABE = \angle DAF$。在$\triangle ABE$和$\triangle DAF$中，
$\left\{\begin{array}{l} \angle EAB = \angle D \\ AB = DA \\ \angle ABE = \angle DAF \end{array}\right.$，
$\therefore \triangle ABE \cong \triangle DAF(ASA)$。
$\therefore BE = AF$。