2025年假期冲冠黑龙江教育出版社八年级数学
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年假期冲冠黑龙江教育出版社八年级数学 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
1.如图,AF是△ABC的角平分线,BD⊥AF交AF的延长线于D,DE//AC,交AB于E,AE与BE相等吗?请说明理由.
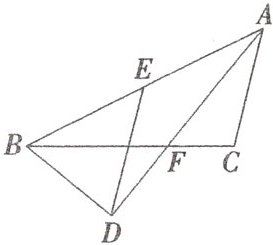

答案:
解:AE = BE。理由如下:
∵AF平分∠BAC,
∴∠EAD = ∠CAD。
∵DE//AC,
∴∠ADE = ∠CAD,
∴∠EAD = ∠ADE,
∴AE = DE。
∵BD⊥AF,
∴∠ADB = 90°,
∴∠EBD + ∠BAD = 90°,∠EDB + ∠ADE = 90°,
∴∠BDE = ∠EBD,
∴BE = ED,
∴AE = BE。
∵AF平分∠BAC,
∴∠EAD = ∠CAD。
∵DE//AC,
∴∠ADE = ∠CAD,
∴∠EAD = ∠ADE,
∴AE = DE。
∵BD⊥AF,
∴∠ADB = 90°,
∴∠EBD + ∠BAD = 90°,∠EDB + ∠ADE = 90°,
∴∠BDE = ∠EBD,
∴BE = ED,
∴AE = BE。
2.如图,△ABC中,AD平分∠BAC,E、F分别在BD、AD上,且DE= CD,EF= AC.求证:EF//AB.
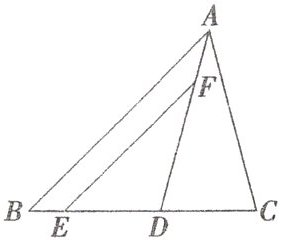

答案:
证明:如图,过$E$作$AC$的平行线,交$AD$的延长线于点$G$,则$\angle DEG=\angle C$,$\angle G=\angle CAD$. 在$\triangle DEG$和$\triangle DCA$中,$\left\{\begin{array}{l} \angle GDE=\angle ADC,\\ ED=CD,\\ \angle DEG=\angle DCA,\end{array}\right.$ $\therefore \triangle DEG≌\triangle DCA(ASA)$,$\therefore EG=CA$. 又$EF = AC$,$\therefore EG = EF$,$\therefore \angle G=\angle EFG=\angle CAD$,$\because AD$平分$\angle BAC$,$\therefore \angle BAD=\angle CAD$,$\therefore \angle EFD=\angle BAD$,$\therefore EF// AB$.

证明:如图,过$E$作$AC$的平行线,交$AD$的延长线于点$G$,则$\angle DEG=\angle C$,$\angle G=\angle CAD$. 在$\triangle DEG$和$\triangle DCA$中,$\left\{\begin{array}{l} \angle GDE=\angle ADC,\\ ED=CD,\\ \angle DEG=\angle DCA,\end{array}\right.$ $\therefore \triangle DEG≌\triangle DCA(ASA)$,$\therefore EG=CA$. 又$EF = AC$,$\therefore EG = EF$,$\therefore \angle G=\angle EFG=\angle CAD$,$\because AD$平分$\angle BAC$,$\therefore \angle BAD=\angle CAD$,$\therefore \angle EFD=\angle BAD$,$\therefore EF// AB$.

3.如图,在△ABC中,AB= AC,点D在AB上,若E在AC的延长线上,且BD= CE,DE交BC于F.求证:DF= EF.


答案:
证明:过点$D$作$DM// AC$交$BC$于点$M$,
$\therefore \angle DMB=\angle ACB$,$\angle FDM=\angle E$,
$\because AB = AC$,
$\therefore \angle B=\angle ACB$,
$\therefore \angle B=\angle DMB$,
$\therefore BD = MD$,
$\because BD = CE$,
$\therefore MD = CE$.
在$\triangle DMF$和$\triangle ECF$中,
$\left\{\begin{array}{l} \angle MDF=\angle E,\\ \angle MFD=\angle CFE,\\ MD=CE,\end{array}\right.$
$\therefore \triangle DMF≌\triangle ECF(AAS)$,
$\therefore DF = EF$.
$\therefore \angle DMB=\angle ACB$,$\angle FDM=\angle E$,
$\because AB = AC$,
$\therefore \angle B=\angle ACB$,
$\therefore \angle B=\angle DMB$,
$\therefore BD = MD$,
$\because BD = CE$,
$\therefore MD = CE$.
在$\triangle DMF$和$\triangle ECF$中,
$\left\{\begin{array}{l} \angle MDF=\angle E,\\ \angle MFD=\angle CFE,\\ MD=CE,\end{array}\right.$
$\therefore \triangle DMF≌\triangle ECF(AAS)$,
$\therefore DF = EF$.
4.如图,在△ABC中,CA= CB,D在AC的延长线上,E在BC上,且CD= CE.求证:DE⊥AB.
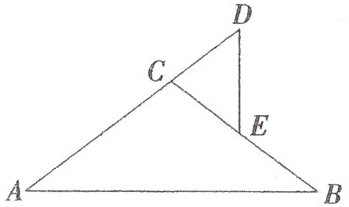

答案:
证明:过点$E$作$EF// AB$交$AC$于点$F$,
$\because CA=CB$,$\therefore \angle A=\angle B$,
$\because EF// AB$,$\therefore \angle CFE=\angle A$,$\angle CEF=\angle B$,
$\therefore \angle CFE=\angle CEF$,
$\because CD=CE$,$\therefore \angle D=\angle CED$,
在$\triangle DEF$中,$\angle D+\angle DEC+\angle DFE+\angle CEF=180^{\circ}$,
又$\angle DFE+\angle CFE=180^{\circ}$,且$\angle CFE=\angle CEF$,
$\therefore \angle D+\angle DEC+\angle CEF+\angle CEF=180^{\circ}$,
$\because \angle D=\angle DEC$,$\therefore 2\angle DEC+2\angle CEF=180^{\circ}$,
$\therefore \angle DEC+\angle CEF=90^{\circ}$,即$\angle DEF=90^{\circ}$,
$\therefore DE\perp EF$,
$\because EF// AB$,$\therefore DE\perp AB$。
$\because CA=CB$,$\therefore \angle A=\angle B$,
$\because EF// AB$,$\therefore \angle CFE=\angle A$,$\angle CEF=\angle B$,
$\therefore \angle CFE=\angle CEF$,
$\because CD=CE$,$\therefore \angle D=\angle CED$,
在$\triangle DEF$中,$\angle D+\angle DEC+\angle DFE+\angle CEF=180^{\circ}$,
又$\angle DFE+\angle CFE=180^{\circ}$,且$\angle CFE=\angle CEF$,
$\therefore \angle D+\angle DEC+\angle CEF+\angle CEF=180^{\circ}$,
$\because \angle D=\angle DEC$,$\therefore 2\angle DEC+2\angle CEF=180^{\circ}$,
$\therefore \angle DEC+\angle CEF=90^{\circ}$,即$\angle DEF=90^{\circ}$,
$\therefore DE\perp EF$,
$\because EF// AB$,$\therefore DE\perp AB$。
查看更多完整答案,请扫码查看


