《2025年课堂笔记六年级数学上册人教版》

典例 王大妈家用篱笆靠墙围了一个半圆形小院，篱笆总长是15.7 m。如果要扩建这个小院，把它的直径增加4 m，那么这个小院的面积增加了多少？

答案：
解题指导 1 画图分析
如图，15.7 m是内圆周长的一半，即$\frac{C}{2}=\pi r=15.7$m，直径增加4 m，就是半径增加2 m，即环宽是2 m，求增加的面积就是求圆环面积的一半。 2 求内半圆和外半圆的半径 内半圆半径：$r=\frac{C}{2}÷\pi=15.7÷3.14=5$（m），外半圆半径：$R=$内半圆半径+环宽。 3 求圆环面积的一半（增加的面积） 圆环面积：$S_{圆环}=\pi(R^2 - r^2)$ 圆环面积的一半：圆环面积÷2 正确解答 原来半圆的半径：15.7÷3.14=5（m） 增加后的半径：5 + 4÷2=7（m） 增加的面积：3.14×(7² - 5²)÷2=37.68（m²） 答：这个小院的面积增加了37.68 m²。

典例 图中涂色部分的面积是100 cm²，求圆环的面积。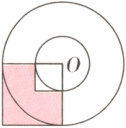解题指导 由图可知：$S_{涂色部分}=S_{大正方形}-S_{小正方形}$ 大正方形的边长=大圆的半径（$R$）→$S_{大正方形}=R^2$ 小正方形的边长=小圆的半径（$r$）→$S_{小正方形}=r^2$ 涂色部分的面积是100 cm²，即$R^2 - r^2=100$（cm²），根据$S_{圆环}=\pi(R^2 - r^2)$可以求出这个圆环的面积。 正确解答 3.14×100=314（cm²） 答：圆环的面积是314 cm²。

答案： 解题指导 由图可知：$S_{涂色部分}=S_{大正方形}-S_{小正方形}$ 大正方形的边长=大圆的半径（$R$）→$S_{大正方形}=R^2$ 小正方形的边长=小圆的半径（$r$）→$S_{小正方形}=r^2$ 涂色部分的面积是100 cm²，即$R^2 - r^2=100$（cm²），根据$S_{圆环}=\pi(R^2 - r^2)$可以求出这个圆环的面积。 正确解答 3.14×100=314（cm²） 答：圆环的面积是314 cm²。