《2026年金考卷中考45套汇编物理河北专版》

17. (6分)小明利用如图11所示的装置探究“浮力大小与哪些因素有关”。他选用一个实心物块、弹簧测力计、水和某液体等进行探究。

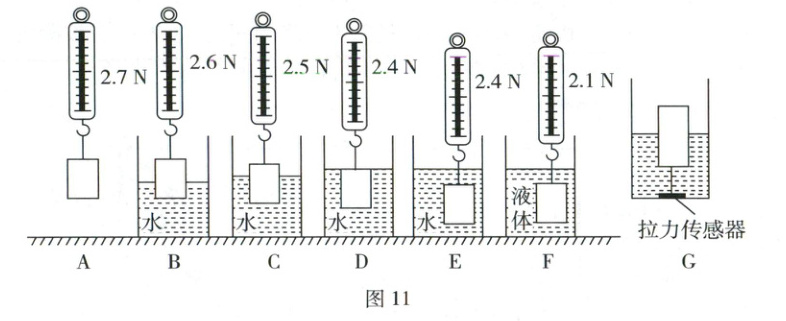
(1)A、B两图中，弹簧测力计示数的变化量等于物块所受浮力的大小。
(2)小明猜想物块在水中受到的浮力大小可能与它浸没的深度和浸入水中的体积有关，根据图A、D、E可知，物块在水中受到的浮力与浸没的深度无关。
(3)图C中，物块下表面受到液体的压力为0.2N。
(4)小明用图中的数据算出了F图中液体的密度为2×10³kg/m³；如果在做图F的实验时不小心使物块接触到了容器底且与容器有力的作用，则此时计算出的液体密度值将偏大(选填“偏大”或“偏小”)。
(5)新考法 利用压力传感器测密度 小明又设计了如图G所示的装置测量木块的密度：往容器中缓慢加水，当木块的一半体积浸入水中时，拉力传感器的示数为$F_{1}$；继续往容器中加水，当木块浸没时，拉力传感器的示数为$F_{2}$。若水的密度为$\rho_{水}$，则木块的密度$\rho_{木}=$$\frac{\rho_{水}(F_2 - 2F_1)}{2(F_2 - F_1)}$(请用$F_{1}$、$F_{2}$、$\rho_{水}$来表示)。

答案： 17.
(1)浮力
(2)浸没的深度
(3)0.2
(4)2×10³ 偏大
(5)$\frac{\rho_{水}(F_2 - 2F_1)}{2(F_2 - F_1)}$
[解题思路]
(1)A图中，F拉A = G物。B图中，物块在竖直向下的重力、竖直向上的浮力和拉力作用下保持静止，则F拉B = G物 - F浮，故F拉A - F拉B = F浮，即A、B两图中弹簧测力计的示数差等于物块所受浮力的大小。
(2)分析D、E的图可知，液体的密度、物块排开液体的体积均相同，物块浸入液体的深度不同，弹簧测力计示数相同，结合图A可知，物块受到的浮力相同，由此可得出浮力大小和物块浸入液体的深度无关。
(3)浸在液体中的物体所受的浮力等于其上下表面受到液体的压力差(F浮 = F向上 - F向下)，图C中物块的上表面未浸入水中(即上表面受到的液体压力为0)，则其下表面受到的液体压力F向上 = F浮 = FA - FC = 2.7N - 2.5N = 0.2N。
(4)根据图A、E可知，物块浸没在水中受到的浮力F浮水 = G物 - F示E = 2.7N - 2.4N = 0.3N，根据图A、F可知，物块浸没在液体中受到的浮力F浮液 = G物 - F示F = 2.7N - 2.1N = 0.6N，因为V排水 = V排液，故根据阿基米德原理可得$\frac{F_{浮水}}{F_{浮液}}$=$\frac{\rho_{水}gV_{排水}}{\rho_{液}gV_{排液}}$，解得ρ液 = $\frac{0.6N}{0.3N}$×ρ水 = $\frac{0.6N}{0.3N}$×1×10³kg/m³ = 2×10³kg/m³。在图F的实验中如果物块受到了容器底部的支持力，则会导致弹簧测力计的读数减小，由F浮液 = G物 - F示F可知，求得F浮液偏大。由ρ液 = $\frac{F_{浮液}}{F_{浮水}}$×ρ水可知计算出的液体的密度会偏大。
(5)木块浸在水中，设木块的重力为G、木块的体积为V、木块受到的浮力为F浮、木块受到的拉力为F拉木，当木块静止时有F浮 = G + F拉木，由于木块受到的拉力等于拉力传感器受到的拉力，也就等于拉力传感器的示数F，即F浮 = G + F。当木块的一半体积浸入水中时，拉力传感器的示数为F₁，则有$\frac{1}{2}$ρ水gV = G + F₁①；当木块浸没时，拉力传感器的示数为F₂，则有ρ水gV = G + F₂②；联立①②可得G = F₂ - 2F₁，V = $\frac{2(F_{2} - F_{1})}{\rho_{水}g}$。由G = mg = ρVg可知，木块的密度ρ木 = $\frac{G}{Vg}$ = $\frac{F_{2} - 2F_{1}}{\frac{2(F_{2} - F_{1})}{\rho_{水}g} × g}$ = $\frac{\rho_{水}(F_{2} - 2F_{1})}{2(F_{2} - F_{1})}$。