《2025年热搜题高中数学选择性必修第二册人教版》

1. [2024·日照质检]记等差数列$\{ a_{n}\}$的前$ n $项和为$ S_{n}$，若$ a_{1}=\dfrac {1}{2}$，$ S_{4}=20$，则$ S_{6}= $(D)

A.16
B.24
C.36
D.48

答案： 1.D 【解析】设$\{ a_{n}\}$的公差为$d$，则$S_{n}=\frac{n}{2}+\frac{n(n - 1)}{2}d$，所以$S_{4}=2 + 6d = 20$，所以$d = 3$，所以$S_{6}=3 + 15d = 48$。故选D。

2. [2024·绍兴模拟]记等差数列$\{ a_{n}\}$的前$ n $项和为$ S_{n}$，$ a_{10}=15$，且$ S_{2}=S_{7}$，则$ a_{8}= $(D)

A.6
B.7
C.8
D.9

答案： 2.D 【解析】设等差数列$\{ a_{n}\}$的公差为$d$，因为$a_{10}=15$，且$S_{2}=S_{7}$，所以$a_{1}+9d = 15$，$2a_{1}+d = 7a_{1}+\frac{7×6}{2}d$，解得$a_{1}=-12$，$d = 3$，则$a_{8}=-12 + 3×7 = 9$。故选D。

3. [2024·马鞍山二中月考]已知$\{ a_{n}\}$为等差数列，公差为$-2$，且$ a_{7}^{2}=a_{3}a_{9}$，则前10项和$ S_{10}=$ 110.

答案： 3.110 【解析】依题意，有$(a_{1}+6d)^{2}=(a_{1}+2d)(a_{1}+8d)$。
因为$d = - 2$，所以$(a_{1}-12)^{2}=(a_{1}-4)(a_{1}-16)$，所以$a_{1}^{2}-24a_{1}+144 = a_{1}^{2}-20a_{1}+64$，解得$a_{1}=20$，所以$S_{10}=$
$10a_{1}+\frac{10×9}{2}d = 10×20 - 90 = 110$。

4. [2024·中山纪念中学月考]设等差数列$\{ a_{n}\}$的前$ n $项和为$ S_{n}$，若$ a_{4}$，$ a_{6}$是方程$ x^{2}-8x+5=0$的两根，则$ S_{9}= $(B)

A.8
B.36
C.45
D.72

答案： 4.B 【解析】由一元二次方程根与系数的关系，可得$a_{4}+a_{6}=8$，所以$S_{9}=\frac{(a_{1}+a_{9})}{2}×9=\frac{(a_{4}+a_{6})}{2}×9=\frac{8}{2}×9 = 36$。故选B。

5. [2024·太原二中期末]记等差数列$\{ a_{n}\}$的前$ n $项和为$ S_{n}$，若$ 3(a_{3}+a_{5})+2(a_{7}+a_{10}+a_{13})=24$，则$ S_{13}= $(C)

A.24
B.25
C.26
D.13

答案： 5.C 【解析】因为$a_{3}+a_{5}=2a_{4}$，$a_{7}+a_{13}=2a_{10}$，所以由已知得$3×2a_{4}+2×3a_{10}=6(a_{4}+a_{10}) = 24$，所以$a_{4}+a_{10}=4$，从而$S_{13}=\frac{13(a_{1}+a_{13})}{2}=\frac{13(a_{4}+a_{10})}{2}=\frac{13×4}{2}=26$。

6. [2024·江西临川一中月考]已知等差数列$\{ a_{n}\}$和等差数列$\{ b_{n}\}$的前$ n $项和分别为$ S_{n}$，$ T_{n}$，且$ (n+1)S_{n}=(7n+23)T_{n}$，则使$\dfrac {a_{n}}{b_{n}}$为整数的正整数$ n $的个数是 (C)

A.2
B.3
C.4
D.5

答案： 6.C 【解析】由题意，可得$\frac{S_{n}}{T_{n}}=\frac{7n + 23}{n + 1}$，则$\frac{a_{n}}{b_{n}}=\frac{2a_{n}}{2b_{n}}=\frac{n(a_{1}+a_{2n - 1})}{2}{÷}\frac{n(b_{1}+b_{2n - 1})}{2}=\frac{S_{2n - 1}}{T_{2n - 1}}=\frac{14n + 16}{2n}=\frac{7n + 8}{n}=7+\frac{8}{n}$，经验证，知当$n = 1,2,4,8$时，$\frac{a_{n}}{b_{n}}$为整数，即使$\frac{a_{n}}{b_{n}}$为整数的正整数$n$的个数是4。故选C。

7. [2024·江苏启东中学月考]已知等差数列$\{ a_{n}\}$的前$ n $项和为$ S_{n}$，且$ S_{6}=36$，$ S_{n}=324$，$ S_{n-6}=144(n ＞ 6)$，则$ n=$ 18.

答案： 7.18 【解析】易知数列$\{ a_{n}\}$的最后6项和为$a_{n}+a_{n - 1}+a_{n - 2}+a_{n - 3}+a_{n - 4}+a_{n - 5}=S_{n}-S_{n - 6}=180$，
因为$a_{1}+a_{2}+a_{3}+a_{4}+a_{5}+a_{6}=36$，
①+②得$6(a_{1}+a_{n}) = 216$，所以$a_{1}+a_{n}=36$。
所以$S_{n}=\frac{n(a_{1}+a_{n})}{2}=\frac{36n}{2}=18n = 324$，所以$n = 18$。

8. [2024·张家港高级中学期中]已知等差数列$\{ a_{n}\}$的前三项为$ a-1$，$ 4$，$ 2a$，记前$ n $项和为$ S_{n}$.
(1)设$ S_{k}=2\ 550$，求$ a $和$ k $的值；
(2)设$ b_{n}=\dfrac {S_{n}}{n}$，求$ b_{3}+b_{7}+b_{11}+·s +b_{4n-1}$的值.

答案： 8.由已知得$4×2 = a - 1 + 2a$，解得$a = 3$，所以$a_{1}=2$，公差$d = a_{2}-a_{1}=2$。
(1)由$S_{k}=ka_{1}+\frac{k(k - 1)}{2}d$，得$2k+\frac{k(k - 1)}{2}×2 = 2550$，
即$k^{2}+k - 2550 = 0$，
解得$k = 50$或$k = - 51$（舍去），
所以$a = 3$，$k = 50$。
(2)由$S_{n}=na_{1}+\frac{n(n - 1)}{2}d$，得$S_{n}=2n+\frac{n(n - 1)}{2}×2=n^{2}+n$，所以$b_{n}=\frac{S_{n}}{n}=n + 1$。
又$b_{3},b_{7},b_{11},·s,b_{4n - 1}$仍是等差数列，且共有$n$项，
所以$b_{3}+b_{7}+b_{11}+·s+b_{4n - 1}=\frac{n(b_{3}+b_{4n - 1})}{2}=\frac{n(4 + 4n)}{2}=2n^{2}+2n$。

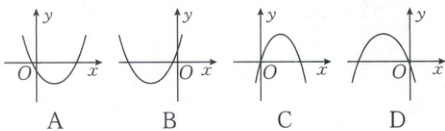
9. [2024·海南中学月考]在等差数列$\{ a_{n}\}$中，首项$ a_{1} ＞ 0$，公差$ d ＜ 0$，$ S_{n}$为其前$ n $项和，则点$ (n,S_{n}) $可能在下列哪条曲线上？(C)

答案： 9.C 【解析】由$S_{n}=na_{1}+\frac{1}{2}n(n - 1)d=\frac{d}{2}n^{2}+(a_{1}-\frac{d}{2})n$
及$d\lt0$，$a_{1}\gt0$知$\frac{d}{2}\lt0$，$a_{1}-\frac{d}{2}\gt0$，对称轴$n=\frac{a_{1}-\frac{d}{2}}{d}\gt0$。故选C。

10. [2024·齐齐哈尔一中月考]设$ S_{n}$是公差为$ d(d\neq 0) $的无穷等差数列$\{ a_{n}\}$的前$ n $项和，则下列命题中错误的是 (C)

A.若$ d ＜ 0$，则数列$\{ S_{n}\}$有最大项
B.若数列$\{ S_{n}\}$有最大项，则$ d ＜ 0$
C.若数列$\{ S_{n}\}$是递增数列，则对任意$ n\in \mathbf{N}^{*}$，均有$ S_{n} ＞ 0$
D.若对任意$ n\in \mathbf{N}^{*}$，均有$ S_{n} ＞ 0$，则数列$\{ S_{n}\}$是递增数列

答案： 10.C 【解析】设$\{ a_{n}\}$的首项为$a_{1}$，则$S_{n}=na_{1}+\frac{1}{2}n·(n - 1)d=\frac{d}{2}n^{2}+(a_{1}-\frac{d}{2})n$。由二次函数的性质知，若$S_{n}$有最大值，则$d\lt0$，故A，B正确；因为$\{ S_{n}\}$为递增数列，所以$d\gt0$。不妨设$a_{1}=-1$，$d = 2$，显然$\{ S_{n}\}$是递增数列，但$S_{1}=-1\lt0$，故C错误；对任意$n\in N^{*}$，$S_{n}$均大于0时，$a_{1}\gt0$，$d\gt0$，$\{ S_{n}\}$必是递增数列，故D正确。故选C。

11. [2024·长春一中期中]设数列$\{ a_{n}\}$的前$ n $项和为$ S_{n}$，点$\left(n,\dfrac {S_{n}}{n}\right)(n\in \mathbf{N}^{*})$均在函数$ y=3x-2 $的图象上，则数列$\{ a_{n}\}$的通项公式$ a_{n}=$ 6n - 5.

答案： 11.6n - 5 【解析】依题意得$\frac{S_{n}}{n}=3n - 2$，即$S_{n}=3n^{2}-2n$，所以数列$\{ a_{n}\}$为等差数列，且$a_{1}=S_{1}=1$，$a_{2}=S_{2}-S_{1}=7$，设其公差为$d$，则$d = 6$，所以$a_{n}=6n - 5(n\in N^{*})$。