《2025年热搜题高中数学选择性必修第二册人教版》

10. 已知$ a \geq \dfrac{1 - x}{x} + \ln x $对任意$ x \in \left[\dfrac{1}{e}, e\right] $恒成立，则$ a $的最小值为(B)

A.$ 1 $
B.$ e - 2 $
C.$ \dfrac{1}{e} $
D.$ 0 $

答案： 10.B[解析]令$f(x)=\frac{1 - x}{x} + \ln x$，$x \in \left[\frac{1}{e}, e\right]$，则$f'(x)=-\frac{1}{x^2} + \frac{1}{x} = \frac{-1 + x}{x^2} = \frac{x - 1}{x^2}$，可得函数$f(x)$在$\left[\frac{1}{e}, 1\right]$上单调递减，在$[1, e]$上单调递增.又$f(e)=\frac{1}{e} ＜ f\left(\frac{1}{e}\right)=e - 2$，所以函数的最大值为$e - 2$，故$a \geqslant e - 2$.故选B.

11. 已知函数$ f(x) = x^3 - 3x - 1 $，若对于区间$ [-3, 2] $上的任意$ x_1, x_2 $都有$ |f(x_1) - f(x_2)| \leq t $，则实数$ t $的最小值是(A)

A.$ 20 $
B.$ 18 $
C.$ 3 $
D.$ 0 $

答案： 11.A[解析]根据题意可得$\vert f(x_1) - f(x_2)\vert \leqslant \vert f(x)_{\max} - f(x)_{\min}\vert \leqslant t$.因为$f'(x)=3x^2 - 3$，$x \in [-3, 2]$，所以$f(x)$在$[-1, 1]$上单调递减，在$[1, 2]$和$[-3, -1]$上单调递增.$f(-3)= -19$，$f(-1)=1$，$f(1)= -3$，$f(2)=1$，所以$\vert f(x)_{\max} - f(x)_{\min}\vert = 20$，所以$t \geqslant 20$.故选A.

12. [2024·福州一中月考]已知曲线$ C: y = \dfrac{1}{3}x^3 - x^2 - 4x + 1 $，直线$ l: x + y + 2k - 1 = 0 $. 若当$ x \in [-3, 3] $时，直线$ l $恒在曲线$ C $的上方，则实数$ k $的取值范围是 $\left(-\infty, -\frac{5}{6}\right)$.

答案： 12.$\left(-\infty, -\frac{5}{6}\right)$[解析]当$x \in [-3, 3]$时，直线$l$恒在曲线C的上方，等价于当$x \in [-3, 3]$时，$(-x - 2k + 1) - \left(\frac{1}{3}x^3 - x^2 - 4x + 1\right) ＞ 0$恒成立，即$k ＜ -\frac{1}{6}x^3 + \frac{1}{2}x^2 + \frac{3}{2}x$.设$f(x)= -\frac{1}{6}x^3 + \frac{1}{2}x^2 + \frac{3}{2}x$ ($x \in [-3, 3]$)，则$f'(x)= -\frac{1}{2}x^2 + x + \frac{3}{2} = \frac{1}{2}(3 - x)(1 + x)$ ($x \in [-3, 3]$).当$x \in [-3, -1)$时，$f'(x) ＜ 0$；当$x \in (-1, 3]$时，$f'(x) ＞ 0$.所以函数$f(x)= -\frac{1}{6}x^3 + \frac{1}{2}x^2 + \frac{3}{2}x$在$[-3, -1)$上单调递减，在$(-1, 3]$上单调递增.所以当$x = -1$时，$f(x)$取得最小值$-\frac{5}{6}$，所以$k ＜ -\frac{5}{6}$.

13. [2024·绵阳中学单元检测]已知函数$ f(x) = \dfrac{m}{x} + \ln x $，$ g(x) = x^3 + x^2 - x $. 若$ m = 3 $，则$ f(x) $的极小值为 ；若对于任意的$ s, t \in \left[\dfrac{1}{2}, 2\right] $，都有$ f(s) \geq \dfrac{1}{10}g(t) $，则实数$ m $的取值范围是 .

答案： 13.$1 + \ln 3$；$[1, +\infty)$[解析]$f(x)$的定义域为$(0, +\infty)$，当$m = 3$时，$f(x)=\frac{3}{x} + \ln x$，则$f'(x)= -\frac{3}{x^2} + \frac{1}{x} = \frac{x - 3}{x^2}$.令$f'(x)=0$，则$x = 3$.所以当$x ＞ 3$时，$f'(x) ＞ 0$，$f(x)$在$(3, +\infty)$上单调递增，当$0 ＜ x ＜ 3$时，$f'(x) ＜ 0$，$f(x)$在$(0, 3)$上单调递减.所以$f(x)$有极小值，为$f(3)=1 + \ln 3$.$g(x)=x^3 + x^2 - x$，$g'(x)=3x^2 + 2x - 1$.当$x \in \left[\frac{1}{2}, 2\right]$时，$g'(x) ＞ 0$，所以$g(x)$在$\left[\frac{1}{2}, 2\right]$上单调递增，所以当$x = 2$时，$g(x)$取得最大值，为$g(2)=10$.对于任意的$s, t \in \left[\frac{1}{2}, 2\right]$，$f(s) \geqslant \frac{1}{10}g(t)$恒成立，即对任意$x \in \left[\frac{1}{2}, 2\right]$，$f(x)=\frac{m}{x} + \ln x \geqslant 1$恒成立，所以对任意的$x \in \left[\frac{1}{2}, 2\right]$，$m \geqslant x - x\ln x$恒成立.令$h(x)=x - x\ln x$，$x \in \left[\frac{1}{2}, 2\right]$，则$h'(x)=1 - \ln x - 1 = -\ln x$，所以当$1 ＜ x \leqslant 2$时，$h'(x) ＜ 0$；当$\frac{1}{2} \leqslant x ＜ 1$时，$h'(x) ＞ 0$.所以$h(x)$在$\left[\frac{1}{2}, 1\right)$上单调递增，在$(1, 2]$上单调递减，所以当$x \in \left[\frac{1}{2}, 2\right]$时，$h(x)$的最大值为$h(1)=1$，所以$m \geqslant 1$，即$m \in [1, +\infty)$.

14. [2024·宁波镇海中学期中]已知$ f(x) = x\mathrm{e}^x $，$ g(x) = -(x + 1)^2 + a $，若$ \exists x_1, x_2 \in \mathbf{R} $，使得$ f(x_2) \leq g(x_1) $成立，则实数$ a $的取值范围是(C)

A.$ [-e, +\infty) $
B.$ (-\infty, -e] $
C.$ \left[-\dfrac{1}{e}, +\infty\right) $
D.$ \left(-\infty, -\dfrac{1}{e}\right] $

答案： 14.C[解析]$\exists x_1, x_2 \in \mathbf{R}$，使得$f(x_2) \leqslant g(x_1)$成立，则$f(x)_{\min} \leqslant g(x)_{\max}$.由题得$f'(x)=e^x + xe^x = (x + 1)e^x$，所以函数$f(x)$在$(-\infty, -1)$上单调递减，在$(-1, +\infty)$上单调递增，所以$f(x)_{\min}=f(-1)= -\frac{1}{e}$.由题得$g(x)_{\max}=g(-1)=a$，所以$a \geqslant -\frac{1}{e}$.

15. 函数$ f(x) = x - \ln(x + 2) + \mathrm{e}^{x - a} + 4\mathrm{e}^{a - x} $，其中$ \mathrm{e} $为自然对数的底数，若存在实数$ x_0 $使$ f(x_0) = 3 $成立，则实数$ a = $ $-\ln 2 - 1$.

答案： 15.$-\ln 2 - 1$[解析]由$f(x)=x - \ln(x + 2) + e^{x - a} + 4e^{-x}$ ($x ＞ -2$)，可令$g(x)=x - \ln(x + 2)$，则$g'(x)=1 - \frac{1}{x + 2} = \frac{x + 1}{x + 2}$，故$g(x)=x - \ln(x + 2)$在$(-2, -1)$上单调递减，在$(-1, +\infty)$上单调递增，故当$x = -1$时，$g(x)$有最小值，为$g(-1)= -1$.又$e^{x - a} + 4e^{-x} \geqslant 4$(当且仅当$e^{x - a}=4e^{-x}$，即$x = a + \ln 2$时，等号成立)，所以$f(x) \geqslant 3$(当且仅当等号同时成立时，等式成立).故$x = a + \ln 2 = -1$，即$a = -\ln 2 - 1$.

16. [2024·长沙一中期末]已知$ f(x) = \ln x - \dfrac{x}{4} + \dfrac{3}{4x} $，$ g(x) = -x^2 - 2ax + 4 $，若对$ \forall x_1 \in (0, 2] $，$ \exists x_2 \in [1, 2] $，使得$ f(x_1) \geq g(x_2) $成立，则$ a $的取值范围是 $\left[-\frac{1}{8}, +\infty\right)$.

答案： 16.$\left[-\frac{1}{8}, +\infty\right)$[解析]因为$f(x)=\ln x - \frac{x}{4} + \frac{3}{4x}$，$x \in (0, 2]$，所以$f'(x)=\frac{1}{x} - \frac{1}{4} - \frac{3}{4x^2} = \frac{-x^2 + 4x - 3}{4x^2} = -\frac{(x - 1)(x - 3)}{4x^2}$，解得$x = 1$ ($x = 3$舍去)，从而当$0 ＜ x ＜ 1$时，$f'(x) ＜ 0$，当$1 ＜ x ＜ 2$时，$f'(x) ＞ 0$，即当$x = 1$时，$f(x)$有最小值，为$\frac{1}{2}$，所以$\exists x \in [1, 2]$，使得$\frac{1}{2} \geqslant -x^2 - 2ax + 4$成立，即$a \geqslant -\frac{x}{2} + \frac{7}{4x}$.因为$y = -\frac{x}{2} + \frac{7}{4x}$在$[1, 2]$上单调递减，所以$y = -\frac{x}{2} + \frac{7}{4x}$的最小值为$-\frac{2}{2} + \frac{7}{8} = -\frac{1}{8}$，所以$a \geqslant -\frac{1}{8}$.

17. [2024·东北育才学校月考]已知函数$ f(x) = x - a\ln x $，$ g(x) = -\dfrac{1 + a}{x} $（$ a \in \mathbf{R} $）.
(1) 设函数$ h(x) = f(x) - g(x) $，求函数$ h(x) $的单调区间；
(2) 若在区间$ [1, e] $上存在一点$ x_0 $，使得$ f(x_0) ＜ g(x_0) $成立，求$ a $的取值范围.

答案： 17.
(1)$h(x)=x + \frac{1 + a}{x} - a\ln x$ ($x ＞ 0$)，$h'(x)=1 - \frac{1 + a}{x^2} - \frac{a}{x} = \frac{x^2 - ax - (1 + a)}{x^2} = \frac{(x + 1)[x - (1 + a)]}{x^2}$.
①当$a + 1 ＞ 0$，即$a ＞ -1$时，在$(0, 1 + a)$上$h'(x) ＜ 0$，在$(1 + a, +\infty)$上$h'(x) ＞ 0$，所以$h(x)$在$(0, 1 + a)$上单调递减，在$(1 + a, +\infty)$上单调递增；
②当$1 + a \leqslant 0$，即$a \leqslant -1$时，在$(0, +\infty)$上$h'(x) ＞ 0$，所以函数$h(x)$在$(0, +\infty)$上单调递增.
综上所述，当$a ＞ -1$时，$h(x)$在$(0, 1 + a)$上单调递减，在$(1 + a, +\infty)$上单调递增；当$a \leqslant -1$时，函数$h(x)$在$(0, +\infty)$上单调递增.
(2)在$[1, e]$上存在一点$x_0$，使得$f(x_0) ＜ g(x_0)$成立，即在$[1, e]$上存在一点$x_0$，使得$h(x_0) ＜ 0$，即函数$h(x)=x + \frac{1 + a}{x} - a\ln x$在$[1, e]$上的最小值小于零.
由
(1)可知：
①当$1 + a \geqslant e$，即$a \geqslant e - 1$时，$h(x)$在$[1, e]$上单调递减，所以$h(x)$的最小值为$h(e)$，由$h(e)=e + \frac{1 + a}{e} - a ＜ 0$可得$a ＞ \frac{e^2 + 1}{e - 1}$.
②当$1 + a \leqslant 1$，即$a \leqslant 0$时，$h(x)$在$[1, e]$上单调递增，所以$h(x)$的最小值为$h(1)$，由$h(1)=1 + 1 + a ＜ 0$可得$a ＜ -2$.
③当$1 ＜ 1 + a ＜ e$，即$0 ＜ a ＜ e - 1$时，可得$h(x)$的最小值为$h(1 + a)$.因为$0 ＜ \ln(1 + a) ＜ 1$，所以$0 ＜ a\ln(1 + a) ＜ a$.故$h(1 + a)=2 + a - a\ln(1 + a) ＞ 2$，此时，$h(1 + a) ＜ 0$不成立.
综上所述，所求$a$的取值范围是$a ＞ \frac{e^2 + 1}{e - 1}$或$a ＜ -2$.

18. [2024·德阳一中月考]已知横梁的强度和它的矩形横断面的长的平方与宽的乘积成正比，要将直径为$ d $的圆木锯成强度最大的横梁，则横断面的长和宽分别为 $\frac{\sqrt{6}}{3}d$，$\frac{\sqrt{3}}{3}d$.

答案：
18.$\frac{\sqrt{6}}{3}d$，$\frac{\sqrt{3}}{3}d$[解析]如图所示，设矩形横断面的宽为$x$，长为$y$，则由题意知，当$xy^2$取最大值时，横梁的强度最大.

因为$y^2 = d^2 - x^2$，所以$xy^2 = x(d^2 - x^2)$ ($0 ＜ x ＜ d$).令$f(x)=x(d^2 - x^2)$ ($0 ＜ x ＜ d$)，则$f'(x)=d^2 - 3x^2$ ($0 ＜ x ＜ d$).令$f'(x)=0$，解得$x = \frac{\sqrt{3}}{3}d$或$x = -\frac{\sqrt{3}}{3}d$(舍去).当$0 ＜ x ＜ \frac{\sqrt{3}}{3}d$时，$f'(x) ＞ 0$；当$\frac{\sqrt{3}}{3}d ＜ x ＜ d$时，$f'(x) ＜ 0$.故当$x = \frac{\sqrt{3}}{3}d$时，$f(x)$取得极大值，也是最大值，所以当矩形横断面的长为$\frac{\sqrt{6}}{3}d$，宽为$\frac{\sqrt{3}}{3}d$时，横梁的强度最大.

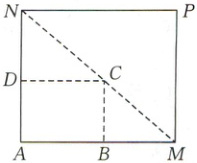
19. [2024·太原五中月考]如图，将一个矩形花坛$ ABCD $扩建成一个更大的矩形花坛$ AMPN $，要求$ B $在$ AM $上，$ D $在$ AN $上，且对角线$ MN $过$ C $点，$ |AB| = 3 \, \mathrm{m} $，$ |AD| = 2 \, \mathrm{m} $.
(1) 当$ AN $的长度是多少时，矩形$ AMPN $的面积最小？求出最小面积；
(2) 若$ AN $的长度不少于$ 6 \, \mathrm{m} $，则当$ AN $的长度是多少时，矩形$ AMPN $的面积最小？求出最小面积.

答案： 19.设AN的长为$x$m ($x ＞ 2$).
因为$\frac{\vert DN\vert}{\vert AN\vert} = \frac{\vert DC\vert}{\vert AM\vert}$，所以$\vert AM\vert = \frac{3x}{x - 2}$，所以$S_{矩形AMPN} = \vert AN\vert · \vert AM\vert = \frac{3x^2}{x - 2}$.
(1)设$S_{矩形AMPN} = y$，则$y = \frac{3x^2}{x - 2} = 3(x - 2) + \frac{12}{x - 2} + 12 \geqslant 2\sqrt{3(x - 2)·\frac{12}{x - 2}} + 12 = 24$.当且仅当$3(x - 2) = \frac{12}{x - 2}$，即$x = 4$时，等号成立，$y = \frac{3x^2}{x - 2}$取得最小值，为$24 m^2$.
(2)令$y = \frac{3x^2}{x - 2}$，则$y' = \frac{6x(x - 2) - 3x^2}{(x - 2)^2} = \frac{3x(x - 4)}{(x - 2)^2}$.所以当$x ＞ 4$时，$y' ＞ 0$，即函数$y = \frac{3x^2}{x - 2}$在$(4, +\infty)$上单调递增，所以函数$y = \frac{3x^2}{x - 2}$在$[6, +\infty)$上也单调递增.所以当$x = 6$时，$y = \frac{3x^2}{x - 2}$取得最小值，即当AN的长度为$6$m时，$S_{矩形AMPN}$取得最小值，为$27 m^2$.