2025年热搜题高中数学选择性必修第二册人教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年热搜题高中数学选择性必修第二册人教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
1. [2024·福州一中期末]已知某质点的运动方程为$ s = 2t^2 - t $,其中$ s $的单位是$ m $,$ t $的单位是$ s $,则该质点在$ 2\ s $末的瞬时速度为(
A.$ 3\ m/s $
B.$ 5\ m/s $
C.$ 7\ m/s $
D.$ 9\ m/s $
C
)A.$ 3\ m/s $
B.$ 5\ m/s $
C.$ 7\ m/s $
D.$ 9\ m/s $
答案:
1.C 【解析$】\lim_{\Delta t \to 0} \frac{\Delta s}{\Delta t} = \lim_{\Delta t \to 0} \frac{2(2 + \Delta t)^2 - (2 + \Delta t) - (2 × 2^2 - 2)}{\Delta t} = $
$\lim_{\Delta t \to 0}(7 + 2\Delta t) = 7,$所以该质点在2s末的瞬时速度为7m/s.
故选C.
$\lim_{\Delta t \to 0}(7 + 2\Delta t) = 7,$所以该质点在2s末的瞬时速度为7m/s.
故选C.
2. [2024·福建师大附中期中](多选)如图所示是物体甲、乙在时间$ 0 $到$ t_1 $范围内,路程的变化情况,下列说法错误的有 (
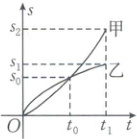
A.在$ 0 $到$ t_0 $范围内,甲的平均速度大于乙的平均速度
B.在$ 0 $到$ t_0 $范围内,甲的平均速度小于乙的平均速度
C.在$ t_0 $到$ t_1 $范围内,甲的平均速度大于乙的平均速度
D.在$ t_0 $到$ t_1 $范围内,甲的平均速度小于乙的平均速度
ABD
)
A.在$ 0 $到$ t_0 $范围内,甲的平均速度大于乙的平均速度
B.在$ 0 $到$ t_0 $范围内,甲的平均速度小于乙的平均速度
C.在$ t_0 $到$ t_1 $范围内,甲的平均速度大于乙的平均速度
D.在$ t_0 $到$ t_1 $范围内,甲的平均速度小于乙的平均速度
答案:
2.ABD 【解析】在0到$t_0$范围内,甲、乙的平均速度都为$\bar{v} = \frac{s_0}{t_0},$故A,B错误.在$t_0$到$t_1$范围内,甲的平均速度为$\frac{s_2 - s_0}{t_1 - t_0},$乙的平均速度为$\frac{s_1 - s_0}{t_1 - t_0}.$因为$s_2 - s_0 > s_1 - s_0,$$t_1 - t_0 > 0,$所以$\frac{s_2 - s_0}{t_1 - t_0} > \frac{s_1 - s_0}{t_1 - t_0},$故C正确,D错误.故选ABD.
3. [2024·信阳二中周练]航天飞机升空后一段时间内,第$ t\ s $时的高度为$ h(t) = 5t^3 + 30t^2 + 45t + 4 $,其中$ h $的单位为$ m $,$ t $的单位为$ s $。
(1)$ h(0) $,$ h(1) $,$ h(2) $分别表示什么?
(2)求第$ 2\ s $内的平均速度;
(3)求第$ 2\ s $末的瞬时速度。
(1)$ h(0) $,$ h(1) $,$ h(2) $分别表示什么?
(2)求第$ 2\ s $内的平均速度;
(3)求第$ 2\ s $末的瞬时速度。
答案:
3.
(1)h
(0)表示航天飞机起飞前的高度;h
(1)表示航天飞机升空后第1s时的高度;h
(2)表示航天飞机升空后第2s时的高度.
(2)航天飞机升空后第2s内的平均速度为
$\bar{v} = \frac{h(2) - h(1)}{2 - 1} = 170(m/s).$
(3)第2s末的瞬时速度为
$\lim_{\Delta t \to 0} \frac{\Delta h}{\Delta t} = \lim_{\Delta t \to 0} \frac{h(2 + \Delta t) - h(2)}{\Delta t}$
$= \lim_{\Delta t \to 0} \frac{5(\Delta t)^3 + 60(\Delta t)^2 + 225\Delta t}{\Delta t}$
= 225(m/s).
(1)h
(0)表示航天飞机起飞前的高度;h
(1)表示航天飞机升空后第1s时的高度;h
(2)表示航天飞机升空后第2s时的高度.
(2)航天飞机升空后第2s内的平均速度为
$\bar{v} = \frac{h(2) - h(1)}{2 - 1} = 170(m/s).$
(3)第2s末的瞬时速度为
$\lim_{\Delta t \to 0} \frac{\Delta h}{\Delta t} = \lim_{\Delta t \to 0} \frac{h(2 + \Delta t) - h(2)}{\Delta t}$
$= \lim_{\Delta t \to 0} \frac{5(\Delta t)^3 + 60(\Delta t)^2 + 225\Delta t}{\Delta t}$
= 225(m/s).
4. [2024·湖北团风中学周练]已知函数$ f(x) = x^2 + 3 $图象上四点$ A(1, f(1)) $,$ B(2, f(2)) $,$ C(3, f(3)) $,$ D(4, f(4)) $,割线$ AB $,$ BC $,$ CD $的斜率分别为$ k_1 $,$ k_2 $,$ k_3 $,则(
A.$ k_1 < k_2 < k_3 $
B.$ k_2 < k_1 < k_3 $
C.$ k_3 < k_2 < k_1 $
D.$ k_1 < k_3 < k_2 $
A
)A.$ k_1 < k_2 < k_3 $
B.$ k_2 < k_1 < k_3 $
C.$ k_3 < k_2 < k_1 $
D.$ k_1 < k_3 < k_2 $
答案:
4.A 【解析$】k_1 = \frac{f(2) - f(1)}{2 - 1} = 7 - 4 = 3,$$k_2 = \frac{f(3) - f(2)}{3 - 2} = 12 - 7 = 5,$$k_3 = \frac{f(4) - f(3)}{4 - 3} = 19 - 12 = 7,$所以$k_1 < k_2 < k_3.$故选A.
5. [2024·阳泉一中单元检测]在曲线$ y = x^2 $上取一点$ (1, 1) $及附近一点$ (1 + \Delta x, 1 + \Delta y) $,则曲线在点$ (1, 1) $处的切线的斜率为(
A.$ \Delta x + \dfrac{1}{\Delta x} + 2 $
B.$ 2 $
C.$ \Delta x + 2 $
D.$ 2 + \Delta x - \dfrac{1}{\Delta x} $
B
)A.$ \Delta x + \dfrac{1}{\Delta x} + 2 $
B.$ 2 $
C.$ \Delta x + 2 $
D.$ 2 + \Delta x - \dfrac{1}{\Delta x} $
答案:
5.B 【解析】设$f(x) = x^2,$则$\lim_{\Delta x \to 0} \frac{f(1 + \Delta x) - f(1)}{\Delta x} = \lim_{\Delta x \to 0} \frac{(1 + \Delta x)^2 - 1}{\Delta x} = \lim_{\Delta x \to 0}(\Delta x + 2) = 2.$故选B.
6. [2024·兰州一中月考]若曲线$ y = x^2 - x + c $上一点$ P $的横坐标是$ -2 $,在点$ P $处的切线恰好过坐标原点$ O $,则实数$ c = $
4
$ $。
答案:
6.4 【解析】抛物线在点P处切线的斜率为
$k = \lim_{\Delta x \to 0} \frac{\Delta y}{\Delta x}$
$= \lim_{\Delta x \to 0} \frac{[(-2 + \Delta x)^2 - (-2 + \Delta x) + c] - (6 + c)}{\Delta x}$
$= \lim_{\Delta x \to 0} \frac{-5\Delta x + (\Delta x)^2}{\Delta x} = -5.$
因为点P的横坐标是-2,所以点P的纵坐标是6 + c,故直线OP的斜率为$\frac{6 + c}{2}.$根据题意有$\frac{6 + c}{2} = -5,$解得
c = 4.
$k = \lim_{\Delta x \to 0} \frac{\Delta y}{\Delta x}$
$= \lim_{\Delta x \to 0} \frac{[(-2 + \Delta x)^2 - (-2 + \Delta x) + c] - (6 + c)}{\Delta x}$
$= \lim_{\Delta x \to 0} \frac{-5\Delta x + (\Delta x)^2}{\Delta x} = -5.$
因为点P的横坐标是-2,所以点P的纵坐标是6 + c,故直线OP的斜率为$\frac{6 + c}{2}.$根据题意有$\frac{6 + c}{2} = -5,$解得
c = 4.
7. 已知函数$ f(x) = -x^2 + x $图象上两点$ A(2, f(2)) $,$ B(2 + \Delta x, f(2 + \Delta x))(\Delta x > 0) $。
(1)若割线$ AB $的斜率不大于$ -1 $,求$ \Delta x $的取值范围;
(2)求函数$ f(x) = -x^2 + x $的图象在点$ A(2, f(2)) $处切线的方程。
(1)若割线$ AB $的斜率不大于$ -1 $,求$ \Delta x $的取值范围;
(2)求函数$ f(x) = -x^2 + x $的图象在点$ A(2, f(2)) $处切线的方程。
答案:
7.
(1)由题意得,割线AB的斜率为
$\frac{\Delta y}{\Delta x} = \frac{f(2 + \Delta x) - f(2)}{\Delta x}$
$= \frac{-(2 + \Delta x)^2 + (2 + \Delta x) - (-4 + 2)}{\Delta x}$
$= \frac{-4\Delta x + \Delta x - (\Delta x)^2}{\Delta x}$
$= -3 - \Delta x,$
由$-3 - \Delta x \leq -1,$得$\Delta x \geq -2.$因为$\Delta x > 0,$所以$\Delta x$的取值范围是$(0, +\infty).$
(2)由
(1)知函数$f(x) = -x^2 + x$的图象在点A(2, f
(2))处切线的斜率为$k = \lim_{\Delta x \to 0} \frac{\Delta y}{\Delta x} = \lim_{\Delta x \to 0}(-3 - \Delta x) = -3.$因为
$f(2) = -2^2 + 2 = -2,$所以切线的方程为y - (-2) = -3(x - 2),即3x + y - 4 = 0.
(1)由题意得,割线AB的斜率为
$\frac{\Delta y}{\Delta x} = \frac{f(2 + \Delta x) - f(2)}{\Delta x}$
$= \frac{-(2 + \Delta x)^2 + (2 + \Delta x) - (-4 + 2)}{\Delta x}$
$= \frac{-4\Delta x + \Delta x - (\Delta x)^2}{\Delta x}$
$= -3 - \Delta x,$
由$-3 - \Delta x \leq -1,$得$\Delta x \geq -2.$因为$\Delta x > 0,$所以$\Delta x$的取值范围是$(0, +\infty).$
(2)由
(1)知函数$f(x) = -x^2 + x$的图象在点A(2, f
(2))处切线的斜率为$k = \lim_{\Delta x \to 0} \frac{\Delta y}{\Delta x} = \lim_{\Delta x \to 0}(-3 - \Delta x) = -3.$因为
$f(2) = -2^2 + 2 = -2,$所以切线的方程为y - (-2) = -3(x - 2),即3x + y - 4 = 0.
查看更多完整答案,请扫码查看


