《2025年热搜题高中数学选择性必修第二册人教版》

1. [2024·银川一中周练]函数$ y = f(x) = x^2 $在区间$ [x_0, x_0 + \Delta x] $上的平均变化率为$ k_1 $，在区间$ [x_0 - \Delta x, x_0] $上的平均变化率为$ k_2 $，则$ k_1 $与$ k_2 $的大小关系为(A)

A.$ k_1 ＞ k_2 $
B.$ k_1 ＜ k_2 $
C.$ k_1 = k_2 $
D.不能确定

答案： 1.A 【解析】$k_1 = \frac{f(x_0 + \Delta x) - f(x_0)}{\Delta x} = \frac{(x_0 + \Delta x)^2 - x_0^2}{\Delta x} = 2x_0 + \Delta x$，$k_2 = \frac{f(x_0) - f(x_0 - \Delta x)}{\Delta x} = \frac{x_0^2 - (x_0 - \Delta x)^2}{\Delta x} = 2x_0 - \Delta x$. 由题意知$\Delta x ＞ 0$，所以$k_1 ＞ k_2$. 故选 A.

2. [2024·绵阳中学月考]若函数$ f(x) = ax + b $在区间$[1, 2]$上的平均变化率为$ 3 $，则$ a = $(C)

A.$ -3 $
B.$ 2 $
C.$ 3 $
D.$ -2 $

答案： 2.C 【解析】根据平均变化率的定义，可知$\frac{\Delta y}{\Delta x} = \frac{(2a + b) - (a + b)}{2 - 1} = a = 3$. 故选 C.

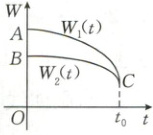
3. [2024·海南中学期末]两个学校甲、乙开展节能活动，活动开始后两学校的用电量$ W_1, W_2 $与时间$ t $(天)的关系如图所示，则一定有(A)


A.学校甲比学校乙节能效果好
B.学校甲的用电量在$[0, t_0]$上的平均变化率比学校乙的用电量在$[0, t_0]$上的平均变化率大
C.两学校节能效果一样好
D.学校甲与学校乙自节能以来用电量总是一样大

答案：
3.A 【解析】连接 AC，BC，如图所示，直线 AC 的倾斜程度大于直线 BC 的倾斜程度，这说明曲线$W_1(t)$比曲线$W_2(t)$下降得快，因此学校甲比学校乙节能效果好，故 A 正确，C 错误；又$\frac{W_1(t_0) - W_1(0)}{t_0} ＜ \frac{W_2(t_0) - W_2(0)}{t_0}$，则学校甲的用电量在$[0, t_0]$上的平均变化率比学校乙的用电量在$[0, t_0]$上的平均变化率要小，故 B 错误；由于曲线$W_1(t)$和曲线$W_2(t)$不重合，故 D 错误. 故选 A.

4. [2024·宜春一中单元检测]已知$ f(x) = -x^2 + 10 $，则$ f(x) $在$ x = \frac{3}{2} $处的瞬时变化率是(B)

A.$ 3 $
B.$ -3 $
C.$ 2 $
D.$ -2 $

答案： 4.B 【解析】因为$\frac{\Delta y}{\Delta x} = \frac{f(\frac{3}{2} + \Delta x) - f(\frac{3}{2})}{\Delta x} = - \Delta x - 3$，所以$\lim_{\Delta x \to 0} \frac{\Delta y}{\Delta x} = - 3$.

5. [2024·东莞检测]若函数$ y = f(x) $在$ x = x_0 $处可导，则$ \lim\limits_{h \to 0} \frac{f(x_0 + h) - f(x_0 - h)}{h} = $(B)

A.$ f'(x_0) $
B.$ 2f'(x_0) $
C.$ -2f'(x_0) $
D.$ 0 $

答案： 5.B 【解析】$\lim_{h \to 0} \frac{f(x_0 + h) - f(x_0 - h)}{h} = \lim_{h \to 0} \left[ 2 × \frac{f(x_0 + h) - f(x_0 - h)}{2h} \right] = 2 \lim_{h \to 0} \frac{f(x_0 + h) - f(x_0 - h)}{2h} = 2f'(x_0)$.

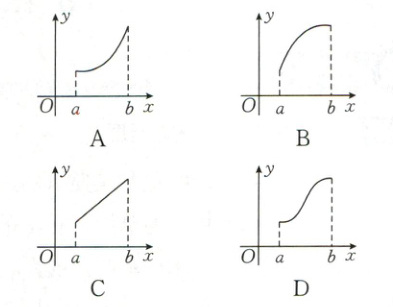
6. [2024·唐山二中月考]若函数$ f(x) $的导函数在区间$[a, b]$上是增函数，则函数$ f(x) $在区间$[a, b]$上的图象可能是(A)

答案： 6.A 【解析】函数$f(x)$的导函数$f'(x)$在$[a, b]$上是增函数，由导数的几何意义可知，曲线$f(x)$在区间$[a, b]$上各点处切线的斜率是逐渐增大的，只有 A 选项符合.

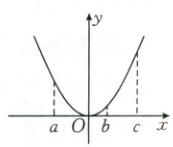
7. [2024·北京四中期末]已知函数$ f(x) $在$ \mathbf{R} $上有导函数，$ f(x) $图象如图所示，则下列不等式正确的是(A)


A.$ f'(a) ＜ f'(b) ＜ f'(c) $
B.$ f'(b) ＜ f'(c) ＜ f'(a) $
C.$ f'(a) ＜ f'(c) ＜ f'(b) $
D.$ f'(c) ＜ f'(a) ＜ f'(b) $

答案： 7.A 【解析】分别作曲线在$x = a$，$x = b$，$x = c$三处的切线$l_1$，$l_2$，$l_3$，设切线的斜率分别为$k_1$，$k_2$，$k_3$. 易知$k_1 ＜ k_2 ＜ k_3$，且$f'(a) = k_1$，$f'(b) = k_2$，$f'(c) = k_3$，所以$f'(a) ＜ f'(b) ＜ f'(c)$. 故选 A.

8. [2024·南宁三中月考]火车开出车站一段时间内，速度$ v $(单位：$ m/s $)与行驶时间$ t $(单位：$ s $)之间的关系是$ v = 0.4t + 0.6t^2 $，则当火车的加速度为$ 2.8 \, m/s^2 $时，行驶时间为2 $ s $。

答案： 8.2 【解析】设火车的加速度为$2.8 m/s^2$时，行驶时间为$t_0 s$，则$\frac{\Delta v}{\Delta t} = \frac{0.4(t_0 + \Delta t) + 0.6(t_0 + \Delta t)^2 - (0.4t_0 + 0.6t_0^2)}{\Delta t} = 0.4 + 1.2t_0 + 0.6\Delta t$，所以$v'(t_0) = \lim_{\Delta t \to 0} \frac{\Delta v}{\Delta t} = \lim_{\Delta t \to 0} (0.4 + 1.2t_0 + 0.6\Delta t) = 0.4 + 1.2t_0 = 2.8$，解得$t_0 = 2$.

9. [2024·武汉二中月考]曲线$ f(x) = \frac{9}{x} $在点$ (3, 3) $处的切线的倾斜角为(C)

A.$ \frac{\pi}{4} $
B.$ \frac{\pi}{3} $
C.$ \frac{3\pi}{4} $
D.$ \frac{2\pi}{3} $

答案： 9.C 【解析】因为$f'(x) = \lim_{\Delta x \to 0} \frac{f(x + \Delta x) - f(x)}{\Delta x} = 9 \lim_{\Delta x \to 0} \frac{\frac{1}{x + \Delta x} - \frac{1}{x}}{\Delta x} = - 9 \lim_{\Delta x \to 0} \frac{1}{(x + \Delta x)x} = - \frac{9}{x^2}$，所以$f'(3) = - 1$. 因为切线的倾斜角的范围为$[0, \pi)$，所以所求倾斜角为$\frac{3\pi}{4}$.

10. [2024·宜昌一中月考](多选)函数$ f(x) = x^3 + x - 2 $的图象在点$ P $处的切线平行于直线$ y = 4x - 1 $，则$ P $点的坐标可以为(AC)

A.$ (1, 0) $
B.$ (2, 8) $
C.$ (-1, -4) $
D.$ (1, 4) $

答案： 10.AC 【解析】因为$f(x) = x^3 + x - 2$，所以$f'(x) = \lim_{\Delta x \to 0} \frac{\Delta y}{\Delta x} = \lim_{\Delta x \to 0} \frac{(x + \Delta x)^3 + (x + \Delta x) - 2 - x^3 - x + 2}{\Delta x} = 3x^2 + 1$. 设$P(x_0, y_0)$，则$f'(x_0) = 3x_0^2 + 1 = 4$，所以$x_0 = \pm 1$. 当$x_0 = 1$时，$f(x_0) = 0$，当$x_0 = - 1$时，$f(x_0) = - 4$，因此$P$点的坐标为$(1, 0)$或$(- 1, - 4)$. 故选 AC.

11. [2024·海口一中周练]已知曲线$ C: y = \frac{1}{3}x^3 + \frac{4}{3} $，则曲线$ C $上横坐标为$ 2 $的点处的切线方程为$4x - y - 4 = 0$。

答案： 11.$4x - y - 4 = 0$ 【解析】将$x = 2$代入曲线 C 的方程，得$y = 4$，所以切点$P(2, 4)$.
$y'|_{x = 2} = \lim_{\Delta x \to 0} \frac{\Delta y}{\Delta x} = \lim_{\Delta x \to 0} \frac{\frac{1}{3}(2 + \Delta x)^3 + \frac{4}{3} - \frac{1}{3} × 2^3 - \frac{4}{3}}{\Delta x} = \lim_{\Delta x \to 0} \left[ 4 + 2\Delta x + \frac{1}{3}(\Delta x)^2 \right] = 4$，所以$k = y'|_{x = 2} = 4$，所以曲线 C 在点$P(2, 4)$处的切线方程为$y - 4 = 4(x - 2)$，即$4x - y - 4 = 0$.