《2025年热搜题高中数学选择性必修第二册人教版》

1. [2024·四川双流中学周练]若$ f'(2)=2 $，则$ \lim\limits_{\Delta x \to 0}\dfrac{f(2)-f(2+\Delta x)}{2\Delta x}= $(C)

A.$-4$
B.$4$
C.$-1$
D.$1$

答案： 1.C【解析】因为$f^{\prime}(2)=2$，所以$\lim_{\Delta x \to 0} \frac{f(2)-f(2 + \Delta x)}{2\Delta x}=$
$-\frac{1}{2}\lim_{\Delta x \to 0} \frac{f(2 + \Delta x)-f(2)}{\Delta x}=-\frac{1}{2}f^{\prime}(2)=-1$。

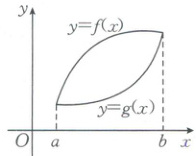
2. 已知函数$ f(x) $和$ g(x) $在区间$[a,b]$上的图象如图所示，则下列说法正确的是 (D)


A.$ f(x) $在$ a $到$ b $之间的平均变化率大于$ g(x) $在$ a $到$ b $之间的平均变化率
B.$ f(x) $在$ a $到$ b $之间的平均变化率小于$ g(x) $在$ a $到$ b $之间的平均变化率
C.对于任意$ x_0 \in (a,b) $，函数$ f(x) $在$ x = x_0 $处的瞬时变化率总大于函数$ g(x) $在$ x = x_0 $处的瞬时变化率
D.存在$ x_0 \in (a,b) $，使得函数$ f(x) $在$ x = x_0 $处的瞬时变化率小于函数$ g(x) $在$ x = x_0 $处的瞬时变化率

答案： 2.D【解析】因为$f(x)$在$a$到$b$之间的平均变化率是$\frac{f(b)-f(a)}{b - a}$，$g(x)$在$a$到$b$之间的平均变化率是$\frac{g(b)-g(a)}{b - a}$，且$f(b)=g(b)$，$f(a)=g(a)$，所以$\frac{f(b)-f(a)}{b - a}=\frac{g(b)-g(a)}{b - a}$，所以A，B错误；易知函数$f(x)$在$x = x_0$处的瞬时变化率是函数$f(x)$在$x = x_0$处的导数，即函数$f(x)$在该点处的切线的斜率，同理函数$g(x)$在$x = x_0$处的瞬时变化率是函数$g(x)$在该点处的导数，即函数$g(x)$在该点处的切线的斜率，由题中图象知C错误，D正确.故选D.

3. (多选)下列命题正确的有 (BD)

A.若$ f'(x_0)=0 $，则函数$ f(x) $在$ x_0 $处无切线
B.函数$ y = f(x) $的切线与函数的图象可以有两个公共点
C.曲线$ y = f(x) $在$ x = 1 $处的切线方程为$ 2x - y = 0 $，则当$ \Delta x \to 0 $时，$ \dfrac{f(1)-f(1+\Delta x)}{2\Delta x}=1 $
D.若函数$ f(x) $的导数$ f'(x)=x^2 - 2 $，且$ f(1)=2 $，则$ f(x) $的图象在$ x = 1 $处的切线方程为$ x + y - 3 = 0 $

答案： 3.BD【解析】若$f^{\prime}(x_0)=0$，则函数$f(x)$在$x_0$处的切线斜率为$0$，故A错误.函数$y = f(x)$的切线与函数的图象可以有两个公共点，例如函数$f(x)=x^3 - 3x$，在$x = 1$处的切线为$y = - 2$，与函数的图象还有一个公共点$(-2,-2)$，故B正确.因为曲线$y = f(x)$在$x = 1$处的切线方程为$2x - y = 0$，所以$f^{\prime}(1)=2$.又$\lim_{\Delta x \to 0} \frac{f(1)-f(1+\Delta x)}{2\Delta x}=$
$-\frac{1}{2}\lim_{\Delta x \to 0} \frac{f(1+\Delta x)-f(1)}{\Delta x}=-\frac{1}{2}f^{\prime}(1)= - 1 \neq 1$，故C错误.因为函数$f(x)$的导数$f^{\prime}(x)=x^2 - 2$，所以$f^{\prime}(1)=$
$1^2 - 2 = - 1$.又$f(1)=2$，所以切点坐标为$(1,2)$，斜率为$-1$，所以切线方程为$y - 2 = -(x - 1)$，化简得$x + y - 3 = 0$，故D正确.故选BD.

4. [2024·榆林一中月考]设$ P $为曲线$ C:y = x^2 + 2x + 3 $上的点，且曲线$ C $在点$ P $处切线的倾斜角的取值范围为$\left[\dfrac{\pi}{4},\dfrac{\pi}{2}\right) $，则点$ P $横坐标的取值范围为 (D)

A.$\left(-\infty,\dfrac{1}{2}\right] $
B.$[-1,0] $
C.$[0,1] $
D.$\left[-\dfrac{1}{2},+\infty\right) $

答案： 4.D【解析】因为$y = x^2 + 2x + 3$，所以
$y^{\prime}=\lim_{\Delta x \to 0} \frac{(x + \Delta x)^2 + 2(x + \Delta x)+3 - (x^2 + 2x + 3)}{\Delta x}$
$=\lim_{\Delta x \to 0} \frac{(2x + 2)· \Delta x + (\Delta x)^2}{\Delta x}$
$=\lim_{\Delta x \to 0} (\Delta x + 2x + 2)=2x + 2$。
因为曲线C在点$P$处切线的倾斜角的取值范围为$[\frac{\pi}{4},\frac{\pi}{2})$，所以其斜率$k \geq 1$.由$y^{\prime}=2x + 2 \in [1,+\infty)$，解得$x \geq -\frac{1}{2}$.故选D.

5. 已知函数$ f(x)=ax^2 + bx + 1(a \neq 0) $在$ x = 0 $处的导数$ f'(0)＞0 $，函数$ f(x) $的图象与$ x $轴恰有一个交点，则$ \dfrac{f(1)}{f'(0)} $的最小值为(A)

A.$ 2 $
B.$\dfrac{3}{2} $
C.$ 3 $
D.$\dfrac{5}{2} $

答案： 5.A【解析】因为$f(x)=ax^2 + bx + 1(a \neq 0)$，所以
$f^{\prime}(0)=\lim_{\Delta x \to 0} \frac{a(0 + \Delta x)^2 + b(0 + \Delta x)+1 - (0 + 0 + 1)}{\Delta x}$
$=\lim_{\Delta x \to 0} (a\Delta x + b)=b＞0$。
因为函数$f(x)$的图象与$x$轴恰有一个交点，所以$b^2 - 4a = 0$，$a = \frac{b^2}{4}$，所以$\frac{f(1)}{f^{\prime}(0)}=\frac{a + b + 1}{b}=\frac{b}{4} + \frac{1}{b}+1 \geq$
$2\sqrt{\frac{b}{4} · \frac{1}{b}} + 1 = 2$，当且仅当$\frac{b}{4}=\frac{1}{b}$，即$b = 2$时，等号成立.故$\frac{f(1)}{f^{\prime}(0)}$的最小值为$2$。

6. [2024·济南二中月考]一物体做直线运动，其位移$ s $与时间$ t $的关系是$ s(t)=3t - t^2 $($ s $的单位：$ \mathrm{m} $，$ t $的单位：$ \mathrm{s} $)，则此物体在$ t = 2\ \mathrm{s} $时的瞬时速度为$-1 m/s$；此物体从$ t = 0\ \mathrm{s} $到$ t = 2\ \mathrm{s} $时的平均速度为$1 m/s$。

答案： 6.$-1 m/s$ $1 m/s$【解析】因为$\frac{s(2 + \Delta t)-s(2)}{\Delta t}=$
$\frac{3(2 + \Delta t)-(2 + \Delta t)^2 - (3×2 - 2^2)}{\Delta t}=-\Delta t - 1$，所以
$\lim_{\Delta t \to 0} \frac{s(2 + \Delta t)-s(2)}{\Delta t}=-1$，所以$t = 2 s$时的瞬时速度为$-1 m/s$.此物体从$t = 0 s$到$t = 2 s$时的平均速度$\overline{v}=$
$\frac{s(2)-s(0)}{2}=\frac{6 - 4 - 0}{2}=1(m/s)$。

7. 已知曲线$ y = x^2 + 1 $，若存在实数$ a $，使得经过点$ (1,a) $能够作出该曲线的两条切线，则实数$ a $的取值范围为$(-\infty,2)$。

答案： 7.$(-\infty,2)$【解析】因为$\frac{\Delta y}{\Delta x}=\frac{(x + \Delta x)^2 + 1 - x^2 - 1}{\Delta x}=2x + \Delta x$，所以$y^{\prime}=\lim_{\Delta x \to 0} \frac{\Delta y}{\Delta x}=\lim_{\Delta x \to 0} (2x + \Delta x)=2x$.设切点$P(x_0,y_0)$，则切线的斜率为$k = y^{\prime}|_{x = x_0}=2x_0$.由点斜式可得所求切线的方程为$y - y_0 = 2x_0(x - x_0)$.又因为切线过点$(1,a)$，且$y_0 = x_0^2 + 1$，所以$a - (x_0^2 + 1)=2x_0(1 - x_0)$，即$x_0^2 - 2x_0 + a - 1 = 0$.因为切线有两条，所以$\Delta = (-2)^2 - 4(a - 1)＞0$，解得$a ＜ 2$.故实数$a$的取值范围是$(-\infty,2)$。

8. 已知气球的体积$ V $（单位：$ \mathrm{L} $）与半径$ r $（单位：$ \mathrm{dm} $）之间的函数关系式是$ V(r)=\dfrac{4}{3}\pi r^3 $。
(1) 求半径$ r $关于体积$ V $的函数$ r(V) $；
(2) 比较气球的体积$ V $从$ 0\ \mathrm{L} $增加到$ 1\ \mathrm{L} $和从$ 1\ \mathrm{L} $增加到$ 2\ \mathrm{L} $的过程中，半径$ r $的平均变化率（精确到$ 0.01 $），哪个过程中半径变化较快？此结论说明什么？（注：$ \sqrt[3]{\dfrac{3}{4\pi}} \approx 0.62 $，$ \sqrt[3]{\dfrac{3}{2\pi}} \approx 0.78 $）

答案： 8.
(1)因为$V(r)=\frac{4}{3}\pi r^3$，
所以$r^3=\frac{3V}{4\pi}$，$r=\sqrt[3]{\frac{3V}{4\pi}}$，所以$r(V)=\sqrt[3]{\frac{3V}{4\pi}}$。
(2)气球的半径$r$在区间$[0,1]$上的平均变化率为$\frac{r(1)-r(0)}{1 - 0} \approx 0.62(dm/L)$。
气球的半径$r$在区间$[1,2]$上的平均变化率为$\frac{r(2)-r(1)}{2 - 1} \approx$
$0.16(dm/L)$。
可以看出，气球的体积$V$从$0 L$增加到$1 L$的过程中，半径变化较快，说明随着气球的体积逐渐变大，气球的半径增加得越来越慢.