2025年热搜题高中数学选择性必修第二册人教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年热搜题高中数学选择性必修第二册人教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
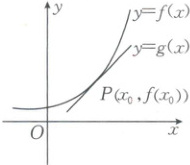
1. 如图所示,可导函数$ y = f(x) $在点$ P(x_0, f(x_0)) $处的切线为$ l:y = g(x) $,设$ h(x) = f(x) - g(x) $,则下列说法正确的是(
A.$ h'(x_0) = 0 $,$ x = x_0 $是$ h(x) $的极大值点
B.$ h'(x_0) = 0 $,$ x = x_0 $是$ h(x) $的极小值点
C.$ h'(x_0) \neq 0 $,$ x = x_0 $不是$ h(x) $的极值点
D.$ h'(x_0) \neq 0 $,$ x = x_0 $是$ h(x) $的极值点
B
)
A.$ h'(x_0) = 0 $,$ x = x_0 $是$ h(x) $的极大值点
B.$ h'(x_0) = 0 $,$ x = x_0 $是$ h(x) $的极小值点
C.$ h'(x_0) \neq 0 $,$ x = x_0 $不是$ h(x) $的极值点
D.$ h'(x_0) \neq 0 $,$ x = x_0 $是$ h(x) $的极值点
答案:
1.B[解析]因为可导函数y=f(x)在点P(x₀,f(x₀))处的切线为l:y=g(x),所以h(x)=f(x)−g(x)在x₀处先减后增,所以h'(x₀)=0,x=x₀是h(x)的极小值点。
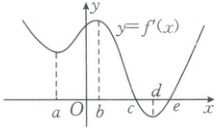
2. [2024·福建仙游一中期末](多选)已知定义在$ \mathbf{R} $上的函数$ f(x) $,其导函数$ f'(x) $的大致图象如图所示,则下列叙述不正确的有(
A.$ f(a) > f(e) > f(d) $
B.函数$ f(x) $在$ [a, b] $上单调递增,在$ [b, d] $上单调递减
C.$ f(x) $的极值点为$ c, e $
D.$ f(x) $的极大值为$ f(b) $
ABD
)
A.$ f(a) > f(e) > f(d) $
B.函数$ f(x) $在$ [a, b] $上单调递增,在$ [b, d] $上单调递减
C.$ f(x) $的极值点为$ c, e $
D.$ f(x) $的极大值为$ f(b) $
答案:
2.ABD[解析]由导数与函数单调性的关系知,当f'(x)>0 时,f(x)单调递增,当f'(x)<0时,f(x)单调递减。由题图可知,当x∈(a,c)时,f'(x)>0,所以f(x)在(a,c)上单调递增;当x∈(c,e)时,f'(x)<0,所以f(x)在(c,e)上单调递减;当x∈(e,+∞)时,f'(x)>0,所以f(x)在(e,+∞)上单调递增。所以函数f(x)在x=c处取得极大值,在x=e处取得极小值,所以f(x)的极值点为c,e。故C正确,A,B,D均不正确。
3. [2024·成都一中月考]设函数$ f(x) $在$ \mathbf{R} $上可导,其导函数为$ f'(x) $,且函数$ f(x) $在$ x = -4 $处取得极小值,则函数$ y = x f'(x) $的图象可能是(
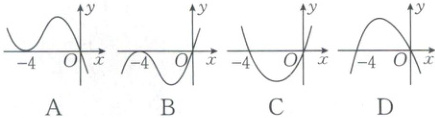
A.图A
B.图B
C.图C
D.图D
C
)
A.图A
B.图B
C.图C
D.图D
答案:
3.C[解析]由函数f(x)在x=−4处取得极小值,可得f'(−4)=0,且导函数f'(x)从左侧趋近−4时,f'(x)<0;从右侧趋近−4时,f'(x)>0。故函数y=xf'(x)从左侧趋近−4时,xf'(x)>0;从右侧趋近−4时,xf'(x)<0。结合所给的选项,可知C正确。
4. [2024·长治二中周练]已知函数$ y = x - \ln(1 + x^2) $,则函数(
A.有极小值
B.有极大值
C.既有极大值也有极小值
D.无极值
D
)A.有极小值
B.有极大值
C.既有极大值也有极小值
D.无极值
答案:
4.D[解析]y'=1−$\frac{2x}{1+x²}$=$\frac{(x−1)²}{1+x²}$,令y'=0,得x=1。当x>1时,y'>0,当x<1时,y'>0,所以函数无极值。故选D。
5. [2024·青岛二中月考]函数$ f(x) = x + 2\cos x $在$ \left[0, \frac{\pi}{2}\right] $上的极大值点为(
A.$ 0 $
B.$ \frac{\pi}{6} $
C.$ \frac{\pi}{3} $
D.$ \frac{\pi}{2} $
B
)A.$ 0 $
B.$ \frac{\pi}{6} $
C.$ \frac{\pi}{3} $
D.$ \frac{\pi}{2} $
答案:
5.B[解析]由题意得,f'(x)=1−2sinx,令f'(x)=0,得x=$\frac{\pi}{6}$。当0<x<$\frac{\pi}{6}$时,f'(x)>0;当$\frac{\pi}{6}$<x<$\frac{\pi}{2}$时,f'(x)<0。所以当x=$\frac{\pi}{6}$时,f(x)取得极大值。
6. [2024·佛山一中期中]若函数$ f(x) = \frac{1}{3}x^3 - \left(1 + \frac{b}{2}\right)x^2 + 2bx $在区间$ [-3, 1] $上不是单调函数,则函数$ f(x) $在$ \mathbf{R} $上的极小值为(
A.$ 2b - \frac{4}{3} $
B.$ \frac{3}{2}b - \frac{2}{3} $
C.$ 0 $
D.$ b^2 - \frac{1}{6}b^3 $
A
)A.$ 2b - \frac{4}{3} $
B.$ \frac{3}{2}b - \frac{2}{3} $
C.$ 0 $
D.$ b^2 - \frac{1}{6}b^3 $
答案:
6.A[解析]f'(x)=x²−(2+b)x+2b=(x−b)(x−2),因为函数f(x)在区间[−3,1]上不是单调函数,所以−3<b<1。由f'(x)>0,得x>2或x<b,由f'(x)<0,得b<x<2,所以f(x)的极小值为f
(2)=$\frac{8}{3}$−(4+2b)+4b=2b−$\frac{4}{3}$。
(2)=$\frac{8}{3}$−(4+2b)+4b=2b−$\frac{4}{3}$。
7. 已知函数$ f(x) = \sqrt{x} - a\ln x $.
(1) 若曲线$ f(x) $在$ x = 1 $处的切线方程为$ x - 2y + 1 = 0 $,求实数$ a $的值;
(2) 求函数$ f(x) $在区间$ [1, 4] $上的极值.
(1) 若曲线$ f(x) $在$ x = 1 $处的切线方程为$ x - 2y + 1 = 0 $,求实数$ a $的值;
(2) 求函数$ f(x) $在区间$ [1, 4] $上的极值.
答案:
7.
(1)因为f(x)=$\sqrt{x}$−alnx,所以f'(x)=$\frac{1}{2\sqrt{x}}$−$\frac{a}{x}$,所以f'
(1)=$\frac{1}{2}$−a。因为曲线f(x)在x=1处的切线方程为x−2y+1=0,所以$\frac{1}{2}$−a=$\frac{1}{2}$,解得a=0。
(2)由
(1),知f'(x)=$\frac{1}{2\sqrt{x}}$−$\frac{a}{x}$=$\frac{\sqrt{x}−2a}{2x}$。
当2a≤1,即a≤$\frac{1}{2}$时,f'(x)≥0在[1,4]上恒成立,所以函数f(x)在[1,4]上单调递增,所以函数f(x)在[1,4]上无极值。
当2a≥2,即a≥1时,f'(x)≤0在[1,4]上恒成立,所以函数f(x)在[1,4]上单调递减,所以函数f(x)在[1,4]上无极值。
当1<2a<2,即$\frac{1}{2}$<a<1时,f'(x),f(x)的变化情况如下表:
x [1,4a²) 4a² (4a²,4]
f'(x) − 0 +
f(x) 单调递减 2a−2aln(2a) 单调递增
所以当x=4a²时,f(x)取得极小值,为2a−2aln(2a),无极大值。
综上所述,当a≤$\frac{1}{2}$或a≥1时,函数f(x)在[1,4]上无极值,当$\frac{1}{2}$<a<1时,函数f(x)在x=4a²时取得极小值,为2a−2aln(2a),无极大值。
(1)因为f(x)=$\sqrt{x}$−alnx,所以f'(x)=$\frac{1}{2\sqrt{x}}$−$\frac{a}{x}$,所以f'
(1)=$\frac{1}{2}$−a。因为曲线f(x)在x=1处的切线方程为x−2y+1=0,所以$\frac{1}{2}$−a=$\frac{1}{2}$,解得a=0。
(2)由
(1),知f'(x)=$\frac{1}{2\sqrt{x}}$−$\frac{a}{x}$=$\frac{\sqrt{x}−2a}{2x}$。
当2a≤1,即a≤$\frac{1}{2}$时,f'(x)≥0在[1,4]上恒成立,所以函数f(x)在[1,4]上单调递增,所以函数f(x)在[1,4]上无极值。
当2a≥2,即a≥1时,f'(x)≤0在[1,4]上恒成立,所以函数f(x)在[1,4]上单调递减,所以函数f(x)在[1,4]上无极值。
当1<2a<2,即$\frac{1}{2}$<a<1时,f'(x),f(x)的变化情况如下表:
x [1,4a²) 4a² (4a²,4]
f'(x) − 0 +
f(x) 单调递减 2a−2aln(2a) 单调递增
所以当x=4a²时,f(x)取得极小值,为2a−2aln(2a),无极大值。
综上所述,当a≤$\frac{1}{2}$或a≥1时,函数f(x)在[1,4]上无极值,当$\frac{1}{2}$<a<1时,函数f(x)在x=4a²时取得极小值,为2a−2aln(2a),无极大值。
查看更多完整答案,请扫码查看


