《2025年热搜题高中数学选择性必修第二册人教版》

5. [2024·衡水二中月考]若各项均为正数的数列$\{a_n\}$满足$a_n^2-(2n-1)a_n-2n=0(n\in\mathbf{N}^*)$,则数列$\{a_n\}$的通项公式$a_n=$$2n$.

答案： 5.$2n$【解析】由$a_{n}^{2}-(2n-1)a_{n}-2n=0$，得$(a_{n}-2n)·(a_{n}+1)=0$.因为$\{a_{n}\}$是正项数列，所以$a_{n}-2n=0$，即$a_{n}=2n$.

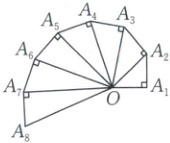
6. [2024·德州检测]如图所示的图形是由一连串直角三角形拼合而成的,其中$OA_1=A_1A_2=A_2A_3=·s=A_7A_8=1$,如果把图中的直角三角形继续作下去,若$OA_1,OA_2,·s,OA_n$的长度构成数列$\{a_n\}$,则此数列的通项公式为$a_n=$$\sqrt{n}$.

]

答案： 6.$\sqrt{n}$【解析】因为$OA_{1}=1$，$OA_{2}=\sqrt{2}$，$OA_{3}=\sqrt{3}$，$·s$，$OA_{n}=\sqrt{n}$，所以$a_{1}=1$，$a_{2}=\sqrt{2}$，$a_{3}=\sqrt{3}$，$·s$，$a_{n}=\sqrt{n}$.

7. [2024·烟台模拟]已知数列$\{a_n\}$的前$n$项和为$S_n$,且满足$S_n=a_n+n^2-1(n\in\mathbf{N}^*)$,则$\{a_n\}$的通项公式为$a_n=$$2n+1$.

答案： 7.$2n + 1$【解析】当$n\geq2$时，$S_{n}=a_{n}+n^{2}-1$，$S_{n-1}=a_{n-1}+(n-1)^{2}-1$，两式相减得$a_{n}=a_{n}-a_{n-1}+2n-1$，即$a_{n-1}=2n-1$，也即$a_{n}=2n + 1(n\geq1)$.所以$\{a_{n}\}$的通项公式为$a_{n}=2n + 1$.

8. [2024·重庆一中月考]在数列$\{a_n\}$中,$a_1=1$,$a_n=n(a_{n+1}-a_n)(n\in\mathbf{N}^*)$,则$a_n=$$n$.

答案： 8.$n$【解析】因为$a_{n}=n(a_{n + 1}-a_{n})$，即$\frac{a_{n + 1}}{a_{n}}=\frac{n + 1}{n}$，所以$\frac{a_{2}}{a_{1}}=\frac{2}{1}$，$\frac{a_{3}}{a_{2}}=\frac{3}{2}$，$\frac{a_{4}}{a_{3}}=\frac{4}{3}$，$·s$，$\frac{a_{n}}{a_{n-1}}=\frac{n}{n-1}(n\geq2)$.以上各式两边分别相乘，得$\frac{a_{n}}{a_{1}}=\frac{2}{1}×\frac{3}{2}×\frac{4}{3}×·s×\frac{n}{n-1}=n(n\geq2)$.又$a_{1}=1$，所以$a_{n}=n(n\geq2)$.因为$a_{1}=1$也适合上式，所以$a_{n}=n$.

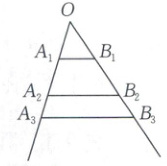
9. [2024·汕头模拟]如图,互不相同的点$A_1,A_2,·s,A_n,·s$和$B_1,B_2,·s,B_n,·s$分别在$\angle O$的两条边上,所有$A_nB_n$相互平行,且所有梯形$A_nB_nB_{n+1}A_{n+1}$的面积均相等.设$OA_n=a_n$.若$a_1=1$,$a_2=2$,则数列$\{a_n\}$的通项公式是$a_n=\sqrt{3n-2}$.

]

答案： 9.$a_{n}=\sqrt{3n - 2}$【解析】令$S_{\triangle OA_{1}B_{1}}=m(m＞0)$，因为所有$A_{n}B_{n}$相互平行，且$a_{1}=1$，$a_{2}=2$，所以$S_{梯形A_{1}B_{1}B_{2}+A_{2}}=S_{梯形A_{1}B_{1}B_{2}A_{2}}=3m$.当$n\geq2$时，$\frac{a_{n}}{a_{n-1}}=\frac{OA_{n}}{OA_{n-1}}=\frac{\sqrt{m+(n-1)×3m}}{\sqrt{m+(n-2)×3m}}=\sqrt{\frac{3n-2}{3n-5}}$，故$\frac{a_{n}^{2}}{a_{n-1}^{2}}=\frac{3n-2}{3n-5}·\frac{a_{n-1}^{2}}{a_{n-2}^{2}}=\frac{3n-8}{3n-11}$，$·s$，$\frac{a_{2}^{2}}{a_{1}^{2}}=\frac{4}{1}$，以上各式累乘可得$\frac{a_{n}^{2}}{a_{1}^{2}}=3n-2(n\geq2)$.因为$a_{1}=1$，且易知$a_{n}＞0$，所以$a_{n}=\sqrt{3n-2}(n\geq2)$.由于$a_{1}=1$满足上式，故$a_{n}=\sqrt{3n-2}$.

10. [2024·六安一中周练]已知点$A_1,A_2,A_3,·s,A_n,·s$和数列$\{a_n\}$,$\{b_n\}$满足$\overrightarrow{A_nA_{n+1}}=\left(\cos\dfrac{2n\pi}{3},\sin\dfrac{2n\pi}{3}\right)(n\in\mathbf{N}^*)$,$a_n\overrightarrow{A_nA_{n+1}}+a_{n+1}\overrightarrow{A_{n+1}A_{n+2}}=(0,b_n)$.若$a_1=1$,$S_n$,$T_n$分别为数列$\{a_n\}$,$\{b_n\}$的前$n$项和,则$S_{60}+2T_{60}=$ (D)

A.-20
B.$24\sqrt{3}$
C.$48\sqrt{3}-20$
D.0

答案： 10.D 【解析】由题意可得$A_{3k-2}A_{3k-1}=(-\frac{1}{2},\frac{\sqrt{3}}{2})$，$A_{3k-1}A_{3k}=(-\frac{1}{2},-\frac{\sqrt{3}}{2})$，$A_{3k}A_{3k + 1}=(1,0)$，则$a_{1}(-\frac{1}{2},\frac{\sqrt{3}}{2})+c_{2}(-\frac{1}{2},-\frac{\sqrt{3}}{2})=(-\frac{1}{2}a_{1}-\frac{1}{2}a_{2},\frac{\sqrt{3}}{2}a_{1}-\frac{\sqrt{3}}{2}a_{2})=(0,b_{1})$.因为$a_{1}=1$，所以$a_{2}=-1$，所以$b_{1}=\sqrt{3}$.由$c_{2}(-\frac{1}{2},-\frac{\sqrt{3}}{2})+a_{3}(1,0)=(-\frac{1}{2}a_{2}+a_{3},-\frac{\sqrt{3}}{2}a_{2})=(0,b_{2})$，得$a_{3}=-\frac{1}{2}$，$b_{2}=\frac{\sqrt{3}}{2}$.同理$a_{4}=-1$，$b_{3}=-\frac{\sqrt{3}}{2}$；$a_{5}=1$，$b_{4}=-\frac{\sqrt{3}}{2}$；$a_{6}=-\frac{1}{2}$，$b_{5}=\frac{\sqrt{3}}{2}$；$a_{7}=1$，$b_{6}=\frac{\sqrt{3}}{2}$；$·s$，即数列$\{a_{n}\}$，$\{b_{n}\}$均是周期为6的数列，且$a_{1}+a_{2}+a_{3}+a_{4}+a_{5}+a_{6}=0$，$b_{1}+b_{2}+b_{3}+b_{4}+b_{5}+b_{6}=0$，所以$S_{60}+2T_{60}=0$.故选D.

11. [2024·东北育才学校期中]已知数列$\{a_n\}$的通项公式为$a_n=\dfrac{n}{n^2+130}(n\in\mathbf{N}^*)$,且数列$\{a_n\}$从第$n$项起单调递减,则$n$的最小值为 (A)

A.11
B.12
C.13
D.不存在

答案： 11.A 【解析】因为$a_{n}=\frac{n}{n^{2}+130}$，所以$a_{n + 1}=\frac{n + 1}{(n + 1)^{2}+130}$，所以$a_{n + 1}-a_{n}=\frac{n + 1}{(n + 1)^{2}+130}-\frac{n}{n^{2}+130}=\frac{-n^{2}-n + 130}{(n^{2}+2n + 131)(n^{2}+130)}$.由数列$\{a_{n}\}$从第$n$项起单调递减可得$a_{n + 1}-a_{n}＜0$，即$-n^{2}-n + 130＜0,n\in\mathbf{N}^{*}$，即$n^{2}+n-130＞0$，解得$n＜\frac{-1-\sqrt{521}}{2}$或$n＞\frac{\sqrt{521}-1}{2}$.又$n\in\mathbf{N}^{*}$，所以$n＞\frac{\sqrt{521}-1}{2}$.因为$22＜\sqrt{521}＜23$，所以$10.5＜\frac{\sqrt{521}-1}{2}＜11$，所以$n\geq11$，所以从第11项起，$\{a_{n}\}$单调递减，所以$n$的最小值为11.故选A.

12. (多选)若数列$\{a_n\}$满足:对任意正整数$n$,$\{a_{n+1}-a_n\}$为递减数列,则称数列$\{a_n\}$为“差递减数列”.给出下列数列$\{a_n\}$的通项公式,其中满足$\{a_n\}$是“差递减数列”的有 (CD)

A.$a_n=3n$
B.$a_n=n^2+1$
C.$a_n=\sqrt{n}$
D.$a_n=\ln\dfrac{n}{n+1}$

答案： 12.CD 【解析】对于A，若$a_{n}=3n$，则$a_{n + 1}-a_{n}=3(n + 1)-3n=3$，所以数列$\{a_{n + 1}-a_{n}\}$不是递减数列，故A错误；对于B，若$a_{n}=n^{2}+1$，则$a_{n + 1}-a_{n}=(n + 1)^{2}+1-n^{2}-1=2n + 1$，所以数列$\{a_{n + 1}-a_{n}\}$是递增数列，故B错误；对于C，若$a_{n}=\sqrt{n}$，则$a_{n + 1}-a_{n}=\sqrt{n + 1}-\sqrt{n}=\frac{1}{\sqrt{n + 1}+\sqrt{n}}$，所以数列$\{a_{n + 1}-a_{n}\}$是递减数列，故C正确；对于D，若$a_{n}=\ln\frac{n}{n + 1}$，则$a_{n + 1}-a_{n}=\ln\frac{n + 1}{n + 2}-\ln\frac{n}{n + 1}=\ln\frac{(n + 1)^{2}}{n(n + 2)}=\ln(1+\frac{1}{n^{2}+2n})$，因为函数$y=\ln(1+\frac{1}{x^{2}+2x})$在$(0,+\infty)$上单调递减，所以数列$\{a_{n + 1}-a_{n}\}$是递减数列，故D正确.故选CD.

13. [2024·岳阳一中月考]已知在数列$\{a_n\}$中,$a_n=1+\dfrac{1}{a+2(n-1)}(n\in\mathbf{N}^*,a\in\mathbf{R},且a\neq0)$.
(1)若$a=-7$,求数列$\{a_n\}$中的最大项和最小项的值；
(2)若对任意的$n\in\mathbf{N}^*$,都有$a_n\leq a_6$成立,求实数$a$的取值范围.

答案： 13.
(1)因为$a_{n}=1+\frac{1}{a+2(n-1)}(n\in\mathbf{N}^{*},a\in\mathbf{R},且a\neq0)$，$a=-7$，所以$a_{n}=1+\frac{1}{2n-9}$.结合函数$f(x)=1+\frac{1}{2x-9}$的单调性，可知$1＞a_{1}＞a_{2}＞a_{3}＞a_{4}＞a_{5}＞a_{6}＞a_{7}＞·s＞a_{n}＞1(n\in\mathbf{N}^{*})$.所以数列$\{a_{n}\}$中的最大项为$a_{5}=2$，最小项为$a_{4}=0$.
(2)$a_{n}=1+\frac{1}{a+2(n-1)}=1+\frac{1}{n-\frac{2-a}{2}}$.因为对任意的$n\in\mathbf{N}^{*}$，都有$a_{n}\leq a_{6}$成立，并结合函数$f(x)=1+\frac{1}{x-\frac{2-a}{2}}$的单调性，所以$5＜\frac{2-a}{2}＜6$，所以$-10＜a＜-8$.故实数$a$的取值范围为$(-10,-8)$.