《2025年热搜题高中数学选择性必修第二册人教版》

1.[2024·广州模拟]函数$ y = \cos(1 + x^2) $的导数$ y' = $(C)

A.$ 2x\sin(1 + x^2) $
B.$ -\sin(1 + x^2) $
C.$ -2x\sin(1 + x^2) $
D.$ 2\cos(1 + x^2) $

答案： 1.C【解析】$y' = [\cos(1 + x^2)]' = -\sin(1 + x^2)(1 + x^2)' = -2x\sin(1 + x^2)$。

2.[2024·黄山检测]函数$ y = (2x + 1)^2 $在$ x = 1 $处的导数值是(D)

A.6
B.8
C.10
D.12

答案： 2.D【解析】因为$y = (2x + 1)^2$，所以$y' = 2(2x + 1)·(2x + 1)' = 4(2x + 1)$，所以$y'|_{x=1} = 4×3 = 12$。

3.[2024·南京模拟]已知函数$ f(x) = \sqrt{ax^2 - 1} $且$ f'(1) = 2 $，则实数$ a $的值为(B)

A.1
B.2
C.$ \sqrt{2} $
D.0

答案： 3.B【解析】因为$f'(x) = \frac{1}{2}(ax^2 - 1)^{-\frac{1}{2}}·2ax = \frac{ax}{\sqrt{ax^2 - 1}}$，所以$f'(1) = \frac{a}{\sqrt{a - 1}} = 2$，所以$a = 2$。故选B。

4.[2024·曲靖一中月考]已知函数$ f(x) $在$ \mathbf{R} $上可导，函数$ F(x) = f(x^2 - 4) + f(4 - x^2) $，则$ F'(2) = $0。

答案： 4.0【解析】因为$F(x) = f(x^2 - 4) + f(4 - x^2)$，所以$F'(x) = 2xf'(x^2 - 4) - 2xf'(4 - x^2)$，所以$F'(2) = 4f'(0) - 4f'(0) = 0$。

5.[2024·南阳一中周练]求导：
(1)$ \left[ \frac{x^2}{(2x + 1)^3} \right]' = $$\frac{2x - 2x^2}{(2x + 1)^4}$；
(2)$ (e^{-x}\sin 2x)' = $$e^{-x}(2\cos2x - \sin2x)$；
(3)$ (\ln\sqrt{2x + 1} - 1)' = $$\frac{1}{2x + 1}$；
(4)$ [\cos(-2x) + 3^{2x + 1}]' = $$-2\sin2x + 2·3^{2x + 1}\ln3$。

答案： 5.
(1)$\frac{2x - 2x^2}{(2x + 1)^4}$
(2)$e^{-x}(2\cos2x - \sin2x)$
(3)$\frac{1}{2x + 1}$
(4)$-2\sin2x + 2·3^{2x + 1}\ln3$
【解析】
(1)$[\frac{x^2}{(2x + 1)^3}]' = \frac{2x·(2x + 1)^3 - x^2·3(2x + 1)^2·2}{(2x + 1)^6} = \frac{2x - 2x^2}{(2x + 1)^4}$。
(2)$(e^{-x}\sin2x)' = -e^{-x}\sin2x + 2e^{-x}\cos2x = e^{-x}(2\cos2x - \sin2x)$。
(3)$(\ln\sqrt{2x + 1} - 1)' = [\frac{1}{2}\ln(2x + 1) - 1]' = \frac{1}{2}×\frac{1}{2x + 1}×(2x + 1)' = \frac{1}{2x + 1}$。
(4)$[\cos(-2x) + 3^{2x + 1}]' = -2\sin2x + (2x + 1)'·3^{2x + 1}\ln3 = -2\sin2x + 2·3^{2x + 1}\ln3$。

6.[2024·哈尔滨二中周练]某市在一次降雨过程中，降雨量$ y(mm) $与时间$ t(min) $的函数关系可近似地表示为$ y = f(t) = \sqrt{10t} $，则在时刻$ t = 40 min $的降雨强度为(D)

A.20 mm/min
B.400 mm/min
C.$ \frac{1}{2} $ mm/min
D.$ \frac{1}{4} $ mm/min

答案： 6.D【解析】由$f(t) = \sqrt{10t}$，得$f'(t) = \frac{1}{2\sqrt{10t}}·(10t)' = \frac{\sqrt{10}}{2\sqrt{t}}$，所以$f'(40) = \frac{\sqrt{10}}{2\sqrt{40}} = \frac{1}{4}$。故选D。

7.[2024·福建仙游一中月考]已知函数$ f(x) = x · \ln ax + b $，曲线$ y = f(x) $在点$ (e, f(e)) $处

的

切线方程为$ y = 2 $，则$ ab = $(C)

A.$ 2 + e^2 $
B.$ 2 + e $
C.$ \frac{2 + e}{e^2} $
D.$ \frac{2}{e^2} $

答案： 7.C【解析】$f'(x) = \ln ax + 1$。由题意得$\begin{cases}f'(e) = 0,\\f(e) = 2,\end{cases}$即$\begin{cases}\ln ae + 1 = 0,\\\ln ae + b = 2,\end{cases}$解得$a = \frac{1}{e^2}$，$b = 2 + e$，所以$ab = \frac{2 + e}{e^2}$。故选C。

8.[2024·宁波一中期中]定义方程$ f(x) = f'(x) $的实数根$ x_0 $为函数$ f(x) $的“新驻点”，若函数$ g(x) = x^2 + 1 $，$ h(x) = \ln(x + 2) $，$ \varphi(x) = \cos x(x \in (0, \pi)) $的“新驻点”分别为$ a $，$ b $，$ c $，则$ a $，$ b $，$ c $的大小关系为(C)

A.$ a ＜ b ＜ c $
B.$ a ＜ c ＜ b $
C.$ b ＜ a ＜ c $
D.$ b ＜ c ＜ a $

答案： 8.C【解析】由$g(x) = x^2 + 1$可得$g'(x) = 2x$，令$x^2 + 1 = 2x$，解得$x_1 = x_2 = 1$，即$a = 1$。由$h(x) = \ln(x + 2)$可得$h'(x) = \frac{1}{x + 2}$，设$F(x) = h(x) - h'(x) = \ln(x + 2) - \frac{1}{x + 2}$，则$F(-1) = -1 ＜ 0$，$F(0) = \ln2 - \frac{1}{2} = \ln\sqrt{4} - \ln\sqrt{e} ＞ 0$，故$-1 ＜ b ＜ 0$。由$\varphi(x) = \cos x(x\in(0,\pi))$可得$\varphi'(x) = -\sin x$，令$\cos x = -\sin x$，得$\sin x + \cos x = 0$，则$\sqrt{2}\sin(x + \frac{\pi}{4}) = 0$。因为$x\in(0,\pi)$，所以$x + \frac{\pi}{4} = \pi$，得$x = \frac{3\pi}{4}$，即$c = \frac{3\pi}{4}$。综上可知，$b ＜ a ＜ c$。故选C。

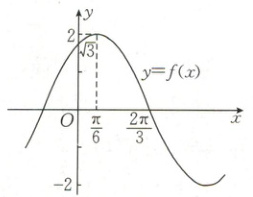
9.[2024·珠海一中月考](多选)已知函数$ f(x) = A\sin(\omega x + \varphi)(A ＞ 0, \omega ＞ 0, |\varphi| ＜ \frac{\pi}{2}) $的图象如图所示，令$ g(x) = f(x) + f'(x) $，则下列关于函数$ g(x) $的说法正确的有(AD)


A.函数$ g(x) $图象的对称轴方程为$ x = k\pi - \frac{\pi}{12}(k \in \mathbf{Z}) $
B.函数$ g(x) $的最大值为2
C.函数$ g(x) $的图象上存在点$ P $，使得在$ P $点处的切线与直线$ l: y = 3x - 1 $平行
D.方程$ g(x) = 2 $的两个不同的解分别为$ x_1 $，$ x_2 $，则$ |x_1 - x_2| $的最小值为$ \frac{\pi}{2} $

答案： 9.AD【解析】根据函数$f(x) = A\sin(\omega x + \varphi)$的图象知$A = 2$，$\frac{T}{4} = \frac{2\pi}{3} - \frac{\pi}{6} = \frac{\pi}{2}$，所以$T = 2\pi$，$\omega = \frac{2\pi}{T} = 1$。
根据五点法知，当$x = \frac{\pi}{6}$时，$\omega x + \varphi = \frac{\pi}{6} + \varphi = \frac{\pi}{2} + 2k\pi$，$k\in\mathbf{Z}$。因为$|\varphi| ＜ \frac{\pi}{2}$，所以$\varphi = \frac{\pi}{3}$，所以$f(x) = 2\sin(x + \frac{\pi}{3})$，所以$f'(x) = 2\cos(x + \frac{\pi}{3})$，所以$g(x) = f(x) + f'(x) = 2\sin(x + \frac{\pi}{3}) + 2\cos(x + \frac{\pi}{3}) = 2\sqrt{2}\sin(x + \frac{\pi}{3} + \frac{\pi}{4}) = 2\sqrt{2}\sin(x + \frac{7\pi}{12})$。令$x + \frac{7\pi}{12} = \frac{\pi}{2} + k\pi$，$k\in\mathbf{Z}$，解得$x = -\frac{\pi}{12} + k\pi$，$k\in\mathbf{Z}$，所以函数$g(x)$图象的对称轴方程为$x = -\frac{\pi}{12} + k\pi$，$k\in\mathbf{Z}$，A正确。
当$x + \frac{7\pi}{12} = \frac{\pi}{2} + 2k\pi$，$k\in\mathbf{Z}$时，函数$g(x)$取得最大值$2\sqrt{2}$，B错误。
因为$g'(x) = 2\sqrt{2}\cos(x + \frac{7\pi}{12})$，所以$g'(x) \leq 2\sqrt{2} ＜ 3$，所以不存在点P，使得在P点处的切线与直线$l: y = 3x - 1$平行，C错误。
方程$g(x) = 2$，即$2\sqrt{2}\sin(x + \frac{7\pi}{12}) = 2$，所以$\sin(x + \frac{7\pi}{12}) = \frac{\sqrt{2}}{2}$，所以$x + \frac{7\pi}{12} = \frac{\pi}{4} + 2k\pi$，$k\in\mathbf{Z}$或$x + \frac{7\pi}{12} = \frac{3\pi}{4} + 2k\pi$，$k\in\mathbf{Z}$，所以当方程的两个不同的解分别为$x_1$，$x_2$时，$|x_1 - x_2|$的最小值为$\frac{\pi}{2}$，D正确。故选AD。

10.[2024·济宁一中期末]设函数$ f(x) = \cos(\sqrt{3}x + \varphi)(0 ＜ \varphi ＜ \pi) $。若$ f(x) + f'(x) $是奇函数，则$ \varphi = $$\frac{\pi}{6}$；若$ f(x) + f'(x) $是偶函数，则$ \varphi = $$\frac{2\pi}{3}$。

答案： 10.$\frac{\pi}{6}$ $\frac{2\pi}{3}$【解析】$f'(x) = -\sqrt{3}\sin(\sqrt{3}x + \varphi)$，$f(x) + f'(x) = \cos(\sqrt{3}x + \varphi) - \sqrt{3}\sin(\sqrt{3}x + \varphi) = 2\sin(\sqrt{3}x + \varphi + \frac{5\pi}{6})$。若$f(x) + f'(x)$为奇函数，则$\varphi + \frac{5\pi}{6} = k\pi(k\in\mathbf{Z})$。因为$\varphi\in(0,\pi)$，所以$\varphi = \frac{\pi}{6}$。若$f(x) + f'(x)$是偶函数，则$\varphi + \frac{5\pi}{6} = k\pi + \frac{\pi}{2}(k\in\mathbf{Z})$。因为$\varphi\in(0,\pi)$，所以$\varphi = \frac{2\pi}{3}$。

11.[2024·金陵中学周练]已知$ a \in \mathbf{R} $，函数$ f(x) = e^x + a · e^{-x} $的导函数是$ f'(x) $，且$ f'(x) $是奇函数。若曲线$ y = f(x) $的一条切线的斜率是$ \frac{3}{2} $，则切点的横坐标$ x_0 = $$\ln2$。

答案： 11.$\ln2$ 2【解析】易得$f'(x) = e^x - ae^{-x}$，$x\in\mathbf{R}$。
因为$f'(x)$为奇函数，所以$f'(x) + f'(-x) = 0$对任意$x\in\mathbf{R}$恒成立，即$(1 - a)(e^x + e^{-x}) = 0$对任意$x\in\mathbf{R}$恒成立，所以$a = 1$，所以$f(x) = e^x + e^{-x}$，$f'(x) = e^x - e^{-x}$。由题可得$e^{x_0} - e^{-x_0} = \frac{3}{2}$，令$e^{x_0} = t(t ＞ 0)$，则$t - \frac{1}{t} = \frac{3}{2}$，解得$t = 2$或$t = -\frac{1}{2}$(舍去)，所以$e^{x_0} = 2$，所以$x_0 = \ln2$。