《2025年热搜题高中数学选择性必修第二册人教版》

1. [2024·湖南师大附中期末](多选)给出定义:若函数$ f(x) $在$ D $上可导,即$ f'(x) $存在,且导函数$ f'(x) $在$ D $上也可导,则称$ f(x) $在$ D $上存在二阶导函数,记$ f''(x)=(f'(x))' $,若$ f''(x)＜0 $在$ D $上恒成立,则称$ f(x) $在$ D $上为凸函数.以下四个函数在$ (0,\frac{\pi}{2}) $上不是凸函数的有 (AD)

A.$ f(x)=\sin x - \cos x $
B.$ f(x)=\ln x - 2x $
C.$ f(x)=-x^3 + 2x - 1 $
D.$ f(x)=xe^x $

答案： 1.AD 【解析】对于$A,f'(x)=\cos x+\sin x,f''(x)=-\sin x+\cos x$，当$x \in (0,\frac{\pi}{4})$时，$f''(x)＞0$，故$f(x)=\sin x-\cos x$不是凸函数；对于$B,f'(x)=\frac{1}{x}-2,f''(x)=-\frac{1}{x^2}＜0$，故$f(x)=\ln x-2x$是凸函数；对于$C,f'(x)=-3x^2+2,f''(x)=-6x$，当$x \in (0,\frac{\pi}{2})$时，$f''(x)＜0$，故$f(x)=$

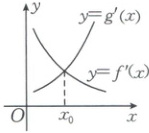
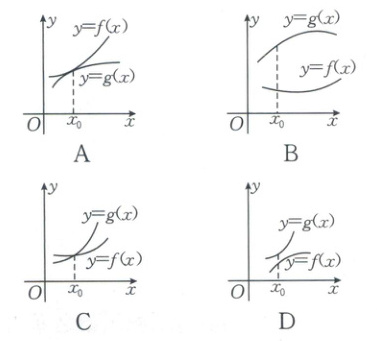
2. [2024·惠州一中期末]如图所示为函数$ y=f(x) $,$ y=g(x) $的导函数的图象,那么$ y=f(x) $,$ y=g(x) $的图象可能是 (D)

答案： 2.D 【解析】由题图知$y=f'(x)$与$y=g'(x)$的图象在$x=x_0$处相交，所以函数$y=f(x)$与$y=g(x)$的图象在$x=x_0$处的切线的斜率相同，排除B,C.又函数$y=f'(x)$中，$y$随$x$的增大而减小，函数$y=g'(x)$中，$y$随$x$的增大而增大，排除A.故选D.

3. 已知$ f(x)=1 + (1 + x) + (1 + x)^2 + (1 + x)^3 + ·s + (1 + x)^n $,则$ f'(0)= $(D)

A.$ n $
B.$ n - 1 $
C.$ \frac{n(n - 1)}{2} $
D.$ \frac{n(n + 1)}{2} $

答案： 3.D 【解析】$f(x)=1+(1+x)+(1+x)^2+(1+x)^3+·s+(1+x)^n$，则$f'(x)=1+2(1+x)+3(1+x)^2+4(1+x)^3+·s+n(1+x)^{n-1}$，则$f'(0)=1+2+3+4+·s+n=\frac{n(n+1)}{2}$.故选D.

4. 已知函数$ f(x) $为$ \mathbf{R} $上的可导函数,其导函数为$ f'(x) $,且$ f(x)=\sqrt{3}f'\left( \frac{\pi}{6} \right)\sin x + \cos x $,在$ \triangle ABC $中,$ f(A)=f'(B)=1 $,则$ \triangle ABC $为 (D)

A.等腰锐角三角形
B.直角三角形
C.等边三角形
D.等腰钝角三角形

答案： 4.D 【解析】因为$f'(x)=\sqrt{3}f'(\frac{\pi}{6})\cos x-\sin x$，所以$f'(\frac{\pi}{6})=\sqrt{3}f'(\frac{\pi}{6})\cos\frac{\pi}{6}-\sin\frac{\pi}{6}=\sqrt{3}×\frac{\sqrt{3}}{2}f'(\frac{\pi}{6})-\frac{1}{2}=\frac{3}{2}f'(\frac{\pi}{6})-\frac{1}{2}$，即$f'(\frac{\pi}{6})=1$，则$f'(x)=\sqrt{3}\cos x-\sin x=2\cos(x+\frac{\pi}{6}),f(x)=\sqrt{3}\sin x+\cos x=2\cos(x-\frac{\pi}{3})$.因为$f'(B)=1$，所以$f'(B)=2\cos(B+\frac{\pi}{6})=1$，即$\cos(B+\frac{\pi}{6})=\frac{1}{2}$.又$B\in(0,\pi)$，所以$B+\frac{\pi}{6}=\frac{\pi}{3}$，解得$B=\frac{\pi}{6}$.因为$f(A)=1$，所以$f(A)=2\cos(A-\frac{\pi}{3})=1$，即$\cos(A-\frac{\pi}{3})=\frac{1}{2}$.又$A\in(0,\pi)$，所以$A-\frac{\pi}{3}=\frac{\pi}{3}$，则$A=\frac{2\pi}{3}$.所以$C=\pi-\frac{2\pi}{3}-\frac{\pi}{6}=\frac{\pi}{6}$，则$B=C$，即$\triangle ABC$是等腰钝角三角形.

5. (多选)已知$ f'(x) $为函数$ f(x) $的导函数,且$ f(x)=\frac{1}{2}x^2 - f(0)x + f'(1)e^{x - 1} $,若$ g(x)=f(x) - \frac{1}{2}x^2 + x $,方程$ g(x) - ax = 0 $有且只有一个根,则$ a $的取值可能是 (ACD)

A.$ e $
B.$ 1 $
C.$ -1 $
D.$ -\frac{1}{2} $

答案： 5.ACD 【解析】因为$f(x)=\frac{1}{2}x^2-f(0)x+f'(1)e^{x-1}$，所以$f(0)=f'(1)e^{-1},f'(x)=x-f(0)+f'(1)e^{x-1}$，所以$f'(1)=1-f'(1)e^{-1}+f'(1)· e^{1-1}$，解得$f'(1)=e$，所以$f(0)=f'(1)e^{-1}=1$，所以$f(x)=\frac{1}{2}x^2-x+e^x$，所以$g(x)=f(x)-\frac{1}{2}x^2+x=e^x-\frac{1}{2}x^2+x=e^x$.因为$g(x)-ax=0$，所以$e^x-ax=0$，即$e^x=ax$.当$a=0$时，$y=e^x$与$y=0$的图象没有交点，关于$x$的方程$e^x-ax=0$无解，不满足条件；当$a＜0$时，$y=e^x$与$y=ax$的图象只有一个交点，关于$x$的方程$e^x-ax=0$有唯一解，满足条件；当$a=e$时，$y=e^x$与$y=ax$的图象相切于一点$(1,e)$，关于$x$的方程$e^x-ax=0$有唯一解，满足条件；当$a＞0$且$a\neq e$时，$y=e^x$与$y=ax$的图象无交点或有两个交点，关于$x$的方程$e^x-ax=0$无解或有两个解，不满足条件.故$a$的取值范围是$a=e$或$a＜0$.故选ACD.

6. [2024·厦门双十中学周练]若数列$ \{c_n\} $为等比数列,其中$ c_1=2 $,$ c_8=4 $,$ f(x)=x(x - c_1)·(x - c_2)··s·(x - c_8) $,$ f'(x) $为函数$ f(x) $的导函数,则$ f'(0)= $$2^{12}$ .

答案： 6.$2^{12}$ 【解析】因为$\{c_n\}$为等比数列，$c_1=2,c_8=4$，所以$c_1c_2·s c_8=8^4=2^{12}.f'(x)=(x-c_1)(x-c_2)·s(x-c_8)+x[(x-c_1)(x-c_2)·s(x-c_8)]'$，则$f'(0)=c_1c_2·s c_8=2^{12}$.

7. [2024·深圳模拟]过点$ M(-1,0) $引曲线$ C:y=2x^3 + ax + a $的两条切线,这两条切线与$ y $轴分别交于$ A $,$ B $两点,若$ |MA|=|MB| $,则$ a= $$-\frac{27}{4}$ .

答案： 7.$-\frac{27}{4}$ 【解析】设切点的坐标为$(t,2t^3+at+a)$，因为$y'=6x^2+a$，所以$6t^2+a=\frac{2t^3+at+a}{t+1}$，即$4t^3+6t^2=0$，解得$t=0$或$t=-\frac{3}{2}$.因为$|MA|=|MB|$，所以$y'|_{x=0}+y'|_{x=-\frac{3}{2}}=0$，即$2a+6×(-\frac{3}{2})^2=0$，解得$a=-\frac{27}{4}$.

8. [2024·重庆南开中学月考]设直线$ l_1 $,$ l_2 $分别是函数$ f(x)=\begin{cases}-\ln x,0＜x＜1, \\ \ln x,x＞1\end{cases}$图象上点$ P_1 $,$ P_2 $处的切线,$ l_1 $与$ l_2 $垂直相交于点$ P $,且$ l_1 $,$ l_2 $分别与$ y $轴相交于点$ A $,$ B $,则$ A $,$ B $两点之间的距离是 ______ .

答案： 8.2 【解析】设$P_1(x_1,f(x_1)),P_2(x_2,f(x_2))$.当$0＜x＜1$时，$f'(x)=-\frac{1}{x}$，当$x＞1$时，$f'(x)=\frac{1}{x}$，故不妨设$x_1\in(0,1),x_2\in(1,+\infty)$，故$l_1:y-(-\ln x_1)=\frac{1}{x_1}(x-x_1)$，整理得到$l_1:y=-\frac{1}{x_1}-\ln x_1+1,l_2:y-\ln x_2=\frac{1}{x_2}(x-x_2)$，整理得到$l_2:y=\frac{1}{x_2}x+\ln x_2-1$，所以$A(0,1-\ln x_1),B(0,\ln x_2-1)$，所以$|AB|=|2-\ln(x_1x_2)|$.因为$l_1\perp l_2$，所以$x_1x_2=1$，所以$|AB|=2$.

9. [2024·长沙一中月考]已知函数$ f(x)=3x + \cos 2x + \sin 2x $,$ f'(x) $是$ f(x) $的导函数,且$ a=f'\left( \frac{\pi}{4} \right) $,求过曲线$ y=x^3 $上一点$ P(a,b) $的切线方程.

答案： 9.由$f(x)=3x+\cos2x+\sin2x$，得$f'(x)=3-2\sin2x+2\cos2x$，则$a=f'(\frac{\pi}{4})=3-2\sin\frac{\pi}{2}+2\cos\frac{\pi}{2}=1$.由$y=x^3$得$y'=3x^2$.当$P$点为切点时，切线的斜率$k=3a^2=3×1^2=3$.又$b=a^3$，所以$b=1$，所以切点$P$的坐标为$(1,1)$，所以曲线$y=x^3$上以点$P$为切点的切线方程为$y-1=3(x-1)$，即$3x-y-2=0$.当$P$点不是切点时，设切点的坐标为$(x_0,x_0^3)$，此时切线的斜率$k'=3x_0^2$，所以切线方程为$y-x_0^3=3x_0^2(x-x_0)$.因为$P(a,b)$在曲线$y=x^3$上，且$a=1$，所以$b=1$，将$P(1,1)$代入切线方程，得$1-x_0^3=3x_0^2(1-x_0)$，所以$2x_0^3-3x_0^2+1=0$，所以$(x_0-1)^2(2x_0+1)=0$，解得$x_0=-\frac{1}{2}(x_0=1舍去)$，所以切点的坐标为$(-\frac{1}{2},-\frac{1}{8})$.又切线的斜率为$3×(-\frac{1}{2})^2=\frac{3}{4}$，所以切线方程为$y+\frac{1}{8}=\frac{3}{4}(x+\frac{1}{2})$，即$3x-4y+1=0$.
综上，满足题意的切线方程为$3x-y-2=0$或$3x-4y+1=0$.