《2025年热搜题高中数学选择性必修第二册人教版》

10. 已知等差数列$ \{a_n\} $的前$ n $项和为$ S_n = n^2 + k + \frac{1}{2}(n\inN^*) $，则$ f(x)=x^3 - kx^2 - 2x + 1 $的极大值为 $\frac{5}{2}$。

答案： 10.$\frac{5}{2}$【解析】因为等差数列前$n$项和公式中常数项为$0$，所以$k+\frac{1}{2}=0$，所以$k=-\frac{1}{2}$，所以$f(x)=x^{3}+\frac{1}{2}x^{2}-2x + 1$，所以$f^{\prime}(x)=3x^{2}+x - 2=(3x - 2)(x + 1)$，所以当$f^{\prime}(x)＞0$时，$x＜-1$或$x＞\frac{2}{3}$，当$f^{\prime}(x)＜0$时，$-1＜x＜\frac{2}{3}$，故函数$f(x)$在$(-\infty,-1)$和$\left(\frac{2}{3},+\infty\right)$上单调递增，在$\left(-1,\frac{2}{3}\right)$上单调递增，故当$x=-1$时，$f(x)$取得极大值，极大值为$f(-1)=\frac{5}{2}$.

11. [2024·东北育才学校月考]设函数$ f'(x) $是奇函数$ f(x)(x\inR) $的导函数，$ f(-1)=0 $，当$ x＞0 $时，$ xf'(x) - f(x)＜0 $，则使得$ f(x)＞0 $成立的$ x $的取值范围是 $(-\infty,-1) \cup (0,1)$。

答案： 11.$(-\infty,-1) \cup (0,1)$【解析】当$x＞0$时，令$F(x)=\frac{f(x)}{x}$，则$F^{\prime}(x)=\frac{xf^{\prime}(x)-f(x)}{x^{2}}＜0$，所以当$x＞0$时，$F(x)=\frac{f(x)}{x}$单调递减.因为$f(x)$为奇函数，且由$f(-1)=0$，得$f(1)=0$，所以$F(1)=0$.在区间$(0,1)$内，$F(x)＞0$；在$(1,+\infty)$内，$F(x)＜0$.即当$0＜x＜1$时，$f(x)＞0$；当$x＞1$时，$f(x)＜0$.又$f(x)$为奇函数，所以当$x \in (-\infty,-1)$时，$f(x)＞0$；当$x \in (-1,0)$时，$f(x)＜0$.综上可知，$f(x)＞0$的解集为$(-\infty,-1) \cup (0,1)$.

12. [2024·衡水中学月考]设函数$ f(x)=\frac{x^2 + 1}{x} $，$ g(x)=\frac{x}{e^x} $，对任意$ x_1, x_2\in(0, +\infty) $，不等式$ \frac{g(x_1)}{k}\leqslant\frac{f(x_2)}{k + 1} $恒成立，则正数$ k $的取值范围是 $\left[\frac{1}{2e - 1},+\infty\right)$。

答案： 12.$\left[\frac{1}{2e - 1},+\infty\right)$【解析】对任意$x_{1},x_{2} \in (0,+\infty)$，不等式$\frac{g(x_{1})}{k} \leq \frac{f(x_{2})}{k + 1}$恒成立等价于$\left(\frac{g(x_{1})}{k}\right)_{\max} \leq \left(\frac{f(x_{2})}{k + 1}\right)_{\min}$.因为$x＞0$，所以$f(x)=\frac{x^{2}+1}{x}=x+\frac{1}{x} \geq 2$.当且仅当$x = 1$时，等号成立，所以$f(x)_{\min}=f(1)=2$，即$\left(\frac{f(x_{2})}{k + 1}\right)_{\min}=\frac{2}{k + 1}$.$g^{\prime}(x)=\frac{3}{2}x^{2}+\frac{3}{2}x - 3+\frac{x - 1}{2e^{x}}=(x - 1)\left(\frac{3}{2}x + 3+\frac{1}{2e^{x}}\right)$.当$x \in (0,1)$时，$g^{\prime}(x)＜0$，当$x \in (1,+\infty)$时，$g^{\prime}(x)＞0$.所以函数$g(x)$在区间$(0,1)$上单调递增，在区间$(1,+\infty)$上单调递减，所以$g(x)_{\max}=g(1)=\frac{1}{e}+\frac{3}{4}+3 + 1-\frac{1}{2e}=\frac{23}{4}-\frac{1}{2e}$，所以$\frac{1}{k} \leq \frac{2}{k + 1}$，所以$\frac{2}{k + 1} \geq \frac{1}{ke}$，解得$k \geq \frac{1}{2e - 1}$.

13. [全国卷Ⅰ]已知函数$ f(x)=\sin x - \ln(1 + x) $，$ f'(x) $为$ f(x) $的导数，证明：
(1) $ f'(x) $在区间$ \left(-1, \frac{\pi}{2}\right) $上存在唯一的极大值点；
(2) $ f(x) $有且仅有2个零点。

答案： 13.证明：
(1)设$g(x)=f^{\prime}(x)$，则$g(x)=\cos x - \frac{1}{1 + x}$.$g^{\prime}(x)=-\sin x+\frac{1}{(1 + x)^{2}}$.当$x \in \left(-1,\frac{\pi}{2}\right)$时，$g^{\prime}(x)$单调递减，而$g^{\prime}(0)＞0$，$g^{\prime}\left(\frac{\pi}{2}\right)＜0$，可得$g^{\prime}(x)$在$\left(-1,\frac{\pi}{2}\right)$上有唯一零点，设为$\alpha\left(0＜\alpha＜\frac{\pi}{2}\right)$.则当$x \in (-1,\alpha)$时，$g^{\prime}(x)＞0$；当$x \in \left(\alpha,\frac{\pi}{2}\right)$时，$g^{\prime}(x)＜0$.所以$g(x)$在$(-1,\alpha)$上单调递增，在$\left(\alpha,\frac{\pi}{2}\right)$上单调递减.故$g(x)$在$\left(-1,\frac{\pi}{2}\right)$上存在唯一的极大值点，即$f^{\prime}(x)$在$\left(-1,\frac{\pi}{2}\right)$上存在唯一的极大值点.
(2)$f(x)$的定义域为$(-1,+\infty)$.①当$x \in (-1,0]$时，由
(1)知，$f^{\prime}(x)$在$(-1,0]$上单调递增，而$f^{\prime}(0)=0$，所以当$x \in (-1,0]$时，$f^{\prime}(x) \leq 0$，故$f(x)$在$(-1,0]$上单调递减.因为$f(0)=0$，所以$x = 0$是$f(x)$在$(-1,0]$上的唯一零点.②当$x \in \left(0,\frac{\pi}{2}\right]$时，由
(1)，$f^{\prime}(x)$在$(0,\alpha)$上单调递增，在$\left(\alpha,\frac{\pi}{2}\right]$上单调递减，而$f^{\prime}(0)=0$，$f^{\prime}\left(\frac{\pi}{2}\right)＜0$，所以存在$\beta \in \left(\alpha,\frac{\pi}{2}\right]$，使得$f^{\prime}(\beta)=0$，且当$x \in (0,\beta)$时，$f^{\prime}(x)＞0$；当$x \in \left(\beta,\frac{\pi}{2}\right]$时，$f^{\prime}(x)＜0$.故$f(x)$在$(0,\beta)$上单调递增，在$\left(\beta,\frac{\pi}{2}\right]$上单调递减.因为$f(0)=0$，$f\left(\frac{\pi}{2}\right)=1-\ln\left(1+\frac{\pi}{2}\right)＞0$，所以当$x \in \left(0,\frac{\pi}{2}\right]$时，$f(x)＞0$.所以$f(x)$在$\left(0,\frac{\pi}{2}\right]$上没有零点.③当$x \in \left[\frac{\pi}{2},\pi\right]$时，$f^{\prime}(x)＜0$，所以$f(x)$在$\left[\frac{\pi}{2},\pi\right]$上单调递减，而$f\left(\frac{\pi}{2}\right)＞0$，$f(\pi)＜0$，所以$f(x)$在$\left[\frac{\pi}{2},\pi\right]$上有唯一零点.④当$x \in (\pi,+\infty)$时，$\ln(x + 1)＞1$，所以$f(x)＜0$，所以$f(x)$在$(\pi,+\infty)$上没有零点.综上所述，$f(x)$有且仅有$2$个零点.

14. [2024·黄冈中学期中]已知函数$ f(x)=\left(a - \frac{1}{2}\right)x^2 + \ln x(a\inR) $。
(1) 当$ a = 1 $时，求$ f(x) $在区间$ [1, e] $上的最大值和最小值；
(2) 若在区间$ (1, +\infty) $上，函数$ f(x) $的图象恒在直线$ y = 2ax $的下方，求实数$ a $的取值范围。

答案： 14.
(1)当$a = 1$时，$f(x)=\frac{1}{2}x^{2}+\ln x$，$f^{\prime}(x)=x+\frac{1}{x}$.当$x \in [1,e]$时，$f^{\prime}(x)＞0$，所以$f(x)$在区间$[1,e]$上单调递增.所以$f(x)_{\max}=f(e)=1+\frac{e^{2}}{2}$，$f(x)_{\min}=f(1)=\frac{1}{2}$.
(2)令$g(x)=f(x)-2ax=\left(a-\frac{1}{2}\right)x^{2}-2ax+\ln x$，则$g(x)$的定义域为$(0,+\infty)$.在区间$(1,+\infty)$上，函数$f(x)$的图象恒在直线$y = 2ax$的下方等价于$g(x)＜0$在区间$(1,+\infty)$上恒成立.$g^{\prime}(x)=(2a - 1)x - 2a+\frac{1}{x}=\frac{(2a - 1)x^{2}-2ax + 1}{x}=\frac{(x - 1)[(2a - 1)x - 1]}{x}$.若$a＞\frac{1}{2}$，令$g^{\prime}(x)=0$，得$x_{1}=1$，$x_{2}=\frac{1}{2a - 1}$，当$x_{2}＞x_{1}=1$，即$\frac{1}{2}＜a＜1$时，在$(x_{2},+\infty)$上有$g^{\prime}(x)＞0$，此时$g(x)$在区间$(x_{2},+\infty)$上单调递增，并且在该区间上有$g(x) \in (g(x_{2}),+\infty)$，不合题意；当$x_{2} \leq x_{1}=1$，即$a \geq 1$时，同理可知，$g(x)$在区间$(1,+\infty)$上单调递增，且$g(x) \in (g(1),+\infty)$，不合题意.若$a \leq \frac{1}{2}$，则有$2a - 1 \leq 0$，此时在区间$(1,+\infty)$上恒有$g^{\prime}(x)＜0$，从而$g(x)$在区间$(1,+\infty)$上单调递减，要使$g(x)＜0$在此区间上恒成立，只需$g(1)=-a-\frac{1}{2} \leq 0$，即$a \geq -\frac{1}{2}$，由此求得实数$a$的取值范围是$\left[-\frac{1}{2},\frac{1}{2}\right]$.综上所述，当$a \in \left[-\frac{1}{2},\frac{1}{2}\right]$时，在区间$(1,+\infty)$上，函数$f(x)$的图象恒在直线$y = 2ax$的下方.

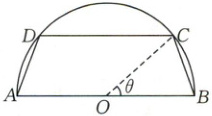
15. [2024·连云港调研]一个圆柱形圆木的底面半径为$ 1\ m $，长为$ 10\ m $，将此圆木沿轴所在的平面剖成两部分。现要把其中一个部分加工成直四棱柱木梁，长度保持不变，底面为等腰梯形$ ABCD $（如图所示，其中$ O $为圆心，$ C, D $在半圆上），设$ \angle BOC = \theta $，木梁的体积为$ V $（单位：$ m^3 $），表面积为$ S $（单位：$ m^2 $）。
(1) 求$ V $关于$ \theta $的函数表达式；
(2) 求$ \theta $的值，使体积$ V $最大；
(3) 问当木梁的体积$ V $最大时，其表面积$ S $是否也最大？请说明理由。

答案： 15.
(1)梯形$ABCD$的面积$S_{梯形ABCD}=\frac{2\cos\theta + 2}{2} · \sin\theta=\sin\theta\cos\theta+\sin\theta$，$\theta \in \left(0,\frac{\pi}{2}\right)$.体积$V(\theta)=10(\sin\theta\cos\theta+\sin\theta)$，$\theta \in \left(0,\frac{\pi}{2}\right)$.
(2)$V^{\prime}(\theta)=10(2\cos^{2}\theta+\cos\theta - 1)=10(2\cos\theta - 1) · (\cos\theta + 1)$.令$V^{\prime}(\theta)=0$，得$\cos\theta=\frac{1}{2}$或$\cos\theta=-1$(舍).因为$\theta \in \left(0,\frac{\pi}{2}\right)$，所以$\theta=\frac{\pi}{3}$.当$\theta \in \left(0,\frac{\pi}{3}\right)$时，$\frac{1}{2}＜\cos\theta＜1$，$V^{\prime}(\theta)＞0$，$V(\theta)$单调递增；当$\theta \in \left(\frac{\pi}{3},\frac{\pi}{2}\right)$时，$0＜\cos\theta＜\frac{1}{2}$，$V^{\prime}(\theta)＜0$，$V(\theta)$单调递减.所以当$\theta=\frac{\pi}{3}$时，体积$V$最大.
(3)木梁的侧面积$S_{侧}=(AB + 2BC + CD) · 10=20\left(\cos\theta+2\sin\frac{\theta}{2}+1\right)$，$\theta \in \left(0,\frac{\pi}{2}\right)$.设$g(\theta)=\cos\theta+2\sin\frac{\theta}{2}+1$，$\theta \in \left(0,\frac{\pi}{2}\right)$.因为$g(\theta)=-2\sin^{2}\frac{\theta}{2}+2\sin\frac{\theta}{2}+2$，所以当$\sin\frac{\theta}{2}=\frac{1}{2}$，即$\theta=\frac{\pi}{3}$时，$g(\theta)$最大.又由
(2)知$\theta=\frac{\pi}{3}$时，$\sin\theta\cos\theta+\sin\theta$取得最大值，所以当$\theta=\frac{\pi}{3}$时，木梁的表面积$S$也最大.综上所述，当木梁的体积$V$最大时，其表面积$S$也最大.

16. [2024·深圳中学月考]已知函数$ f(x)=x^2 - 8\ln x $，$ g(x)= -x^2 + 14x $。
(1) 求函数函数函数\函数\函数\函数\$ f(x)在点$ (1, f(1))处的切线方程；
(2) 若函数$ f(x) $与$ g(x) $在区间$ (a, a + 1) $上均单调递增，求$ a $的取值范围；
(3) 若方程$ f(x) = g(x) + m $有唯一解，试求实数$ m $的值。

答案： 16.
(1)因为$f^{\prime}(x)=2x-\frac{8}{x}$，所以切线的斜率$k = f^{\prime}(1)=-6$.又因为$f(1)=1$，所以所求的切线方程为$y - 1=-6(x - 1)$，即$y=-6x + 7$.
(2)因为$f^{\prime}(x)=\frac{2(x + 2)(x - 2)}{x}$，且$x＞0$，所以当$x＞2$时，$f^{\prime}(x)＞0$；当$0＜x＜2$时，$f^{\prime}(x)＜0$.即$f(x)$在$(2,+\infty)$上单调递增，在$(0,2)$上单调递减.又$g(x)=-(x - 7)^{2}+49$，所以$g(x)$在$(-\infty,7)$上单调递增，在$(7,+\infty)$上单调递减.欲使函数$f(x)$与$g(x)$在区间$(a,a + 1)$上均单调递增，则$\begin{cases}a \geq 2,\\a + 1 \leq 7,\end{cases}$解得$2 \leq a \leq 6$.故$a$的取值范围为$[2,6]$.
(3)原方程等价于$2x^{2}-8\ln x - 14x = m$，令$h(x)=2x^{2}-8\ln x - 14x$，则原方程即为$h(x)=m$.因为当$x＞0$时原方程有唯一解，所以函数$y = h(x)$与$y = m$的图象在$y$轴右侧有唯一的交点.$h^{\prime}(x)=4x-\frac{8}{x}-14=\frac{2(x - 4)(2x + 1)}{x}$，且$x＞0$，所以当$x＞4$时，$h^{\prime}(x)＞0$；当$0＜x＜4$时，$h^{\prime}(x)＜0$.即$h(x)$在$(4,+\infty)$上单调递增，在$(0,4)$上单调递减，故$h(x)$在$x = 4$处取得最小值，从而当$x＞0$时原方程有唯一解的充要条件是$m = h(4)=-16\ln 2 - 24$.