《2025年热搜题高中数学选择性必修第二册人教版》

1. [2024·湛江一中月考]已知数列$\{ a_{n}\} $是等比数列,数列$\{ b_{n}\} $是等差数列,若$a_{1}a_{6}a_{11}=-3\sqrt {3},$$b_{1}+b_{6}+b_{11}=7π$,则$\tan\frac {b_{3}+b_{9}}{1-a_{4}a_{8}}$的值是(A)

A.$-\sqrt {3}$
B.$\frac {\sqrt {2}}{2}$
C.$-\frac {\sqrt {2}}{2}$
D.$\sqrt {3}$

答案： 1.A【解析】因为$\{a_n\}$是等比数列，所以$a_1a_6a_{11}=a_6^3=-3\sqrt{3}$，
所以$a_6=-\sqrt{3}$，所以$a_4a_8=a_6^2=3$.因为$\{b_n\}$是等差数列，
所以$b_1+b_6+b_{11}=3b_6=7\pi$，所以$b_6=\frac{7\pi}{3}$，所以$b_3+b_9=$
$2b_6=\frac{14\pi}{3}$.所以$\frac{b_3+b_9}{1-a_4a_8}=\frac{\frac{7\pi}{3}}{1-3}=-\frac{7\pi}{6}$，所以$\tan\frac{b_3+b_9}{1-a_4a_8}=$
$\tan(-\frac{7\pi}{3})=-\tan\frac{\pi}{3}=-\sqrt{3}$.

2. [2024·运城模拟]已知等比数列$\{ a_{n}\} $的前$n$项和为$S_{n}$,且满足$a_{2},2a_{5},3a_{8}$构成等差数列,则$\frac {3S_{3}}{S_{6}}=$(A)

A.$\frac {9}{4}$或$\frac {3}{2}$
B.$\frac {13}{12}$或$3$
C.$\frac {9}{4}$
D.$\frac {13}{12}$或$\frac {3}{2}$

答案： 2.A【解析】由条件得$a_2+3a_8=4a_5$，即$a_2+3a_2q^6=4a_2q^3$，
即$3q^6-4q^3+1=0$，解得$q^3=1$或$q^3=\frac{1}{3}$.当$q^3=1$时，
$q=1$，$S_6=2S_3$，则$\frac{3S_3}{S_6}=\frac{3}{2}$；当$q^3=\frac{1}{3}$时，$\frac{3S_3}{S_6}=$
$\frac{3a_1(1-q^3)}{a_1(1-q^6)}=\frac{3(1-q^3)}{1-q^6}=\frac{3}{1+q^3}=\frac{3}{1+\frac{1}{3}}=\frac{9}{4}$.故选A.

3. [2024·鞍山一中月考]设$x\in \mathbf{R}$,记不超过$x$的最大整数为$[x]$,如$[2.5]=2,[-2.5]=$$-3$,令$\{ x\} =x-[x]$,则$\left\{ \frac {\sqrt {5}+1}{2}\right\} ,\left[ \frac {\sqrt {5}+1}{2}\right] ,$$\frac {\sqrt {5}+1}{2}$三个数构成的数列(A)

A.是等比数列但不是等差数列
B.是等差数列但不是等比数列
C.既是等差数列又是等比数列
D.既不是等差数列也不是等比数列

答案： 3.A【解析】因为$\left[\frac{\sqrt{5}+1}{2}\right]=1$，所以$\left[\frac{\sqrt{5}+1}{2}\right]=\frac{\sqrt{5}+1}{2}$
$\left[\frac{\sqrt{5}+1}{2}\right]=\frac{\sqrt{5}+1}{2}-1=\frac{\sqrt{5}-1}{2}$.因为$\frac{\sqrt{5}-1}{2}×\frac{\sqrt{5}+1}{2}=1^2$，
$\frac{\sqrt{5}-1}{2}+\frac{\sqrt{5}+1}{2}=\sqrt{5}\neq2×1$，所以$\frac{\sqrt{5}-1}{2},1,\frac{\sqrt{5}+1}{2}$是等比
数列，不是等差数列，即$\left[\frac{\sqrt{5}+1}{2}\right],\left[\frac{\sqrt{5}+1}{2}\right],\frac{\sqrt{5}+1}{2}$是等比
数列，不是等差数列.

4. [2024·武汉一中期中](多选)在公比$q$为整数的等比数列$\{ a_{n}\} $中,$S_{n}$是数列$\{ a_{n}\} $的前$n$项和,若$a_{1}a_{4}=32,a_{2}+a_{3}=12$,则下列说法正确的有(ABC)

A.$q=2$
B.数列$\{ S_{n}+2\} $是等比数列
C.$S_{8}=510$
D.数列$\{ \log _{2}a_{n}\} $是公差为$2$的等差数列

答案： 4.ABC【解析】因为数列$\{a_n\}$为等比数列，$a_1a_4=32$，所以
$a_2a_3=32$.由$\begin{cases}a_2+a_3=12\\a_2a_3=32\end{cases}$，得$\begin{cases}a_2=4\\a_3=8\end{cases}$或$\begin{cases}a_2=8\\a_3=4\end{cases}$.又公比$q$
为整数，所以$\begin{cases}a_2=4\\a_3=8\end{cases}$，所以$a_n=2^n$，$S_n=\frac{2×(1-2^n)}{1-2}=$
$2^{n+1}-2$.易知A正确.对于B，$S_n+2=2^{n+1}$，
$\frac{S_{n+1}+2}{S_n+2}=\frac{2^{n+2}}{2^{n+1}}=2$，所以数列$\{S_n+2\}$是等比数列，故B正确.对于C，
$S_8=2^9-2=510$，故C正确.对于D，$\log_2a_{n+1}-\log_2a_n=$
$(n+1)-n=1$，即数列$\{\log_2a_n\}$是公差为1的等差数列，故
D错误.故选ABC.

5. [2024·遵义四中期中]已知在数列$\{ a_{n}\} $中,$a_{n}=-4n+5$,等比数列$\{ b_{n}\} $的公比$q$满足$q=a_{n}-a_{n-1}(n\geqslant 2)$,且$b_{1}=a_{2}$,则$|b_{1}|+$$|b_{2}|+·s +|b_{n}|=$(B)

A.$1-4^{n}$
B.$4^{n}-1$
C.$\frac {1-4^{n}}{3}$
D.$\frac {4^{n}-1}{3}$

答案： 5.B【解析】因为$q=a_n-a_{n-1}=-4$，$b_1=a_2=-3$，所以$b_n=$
$b_1q^{n-1}=-3×(-4)^{n-1}$，所以$|b_n|=|-3×(-4)^{n-1}|=$
$3×4^{n-1}$，即$\{|b_n|\}$是首项为3，公比为4的等比数列，所以
$|b_1|+|b_2|+·s+|b_n|=\frac{3(1-4^n)}{1-4}=4^n-1$.故选B.

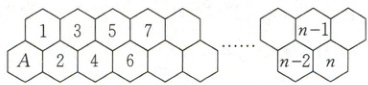
6. [2024·湖州中学期末]一只蜜蜂从蜂房$A$出发向右爬,每次只能爬向右侧相邻的两个蜂房(如图),例如:从蜂房$A$只能爬到$1$号或$2$号蜂房,从$1$号蜂房只能爬到$2$号或$3$号蜂房……以此类推,用$a_{n}$表示蜜蜂爬到$n$号蜂房的方法数,则$a_{2\ 022}a_{2\ 024}-a_{2\ 023}^{2}=$(A)


A.$1$
B.$-1$
C.$2$
D.$-2$

答案： 6.A【解析】由题意可得，$a_1=1$，$a_2=2$，$a_3=a_1+a_2=3$，$a_4=$
$a_2+a_3=5$，$·s$，所以$a_{n+1}=a_n+a_{n-1}(n\in N^*,n\geq2)$，则
$a_1a_3-a_2^2=-1$，$a_2a_4-a_3^2=1$，$a_3a_5-a_4^2=a_3(a_3+a_4)-$
$a_4^2=-1$，$a_4a_6-a_5^2=a_4(a_4+a_5)-a_5^2=1$，猜想：数列
$\{a_na_{n+2}-a_{n+1}^2\}$是首项为-1，公比为-1的等比数列.下面
证明：当$n\geq2$时，$a_na_{n+2}-a_{n+1}^2=a_n(a_{n+1}+a_n)-a_{n+1}^2=$
$a_na_{n+1}+a_n^2-a_{n+1}^2=a_{n+1}(a_n-a_{n+1})+a_n^2=-a_{n+1}a_{n-1}+$
$a_n^2$，即$\frac{a_na_{n+2}-a_{n+1}^2}{a_{n-1}a_{n+1}-a_n^2}=-1$，则$\{a_na_{n+2}-a_{n+1}^2\}$是首项为-1，
公比为-1的等比数列，所以$a_{2022}a_{2024}-a_{2023}^2=(-1)×$
$(-1)^{2021}=1$.故选A.

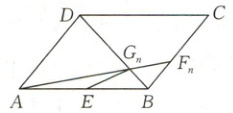
7. [2024·武汉二中月考](多选)如图所示,已知点$E$是平行四边形$ABCD$的边$AB$的中点,$F_{n}(n\in \mathbf{N}^{*})$为边$BC$上的一列点,连接$AF_{n}$交$BD$于$G_{n}$,点$G_{n}(n\in \mathbf{N}^{*})$满足$\overrightarrow {G_{n}D}=$$a_{n+1}· \overrightarrow {G_{n}A}-2(2a_{n}+3)· \overrightarrow {G_{n}E}$,其中数列$\{ a_{n}\} $是首项为$1$的正项数列,$S_{n}$是数列$\{ a_{n}\} $的前$n$项和,则下列结论正确的有(AB)


A.$a_{3}=13$
B.数列$\{ a_{n}+3\} $是等比数列
C.$a_{n}=4n-3$
D.$S_{n}=2^{n+1}-n-2$

答案： 7.AB【解析】因为E为AB的中点，所以$2\overrightarrow{G_nE}=\overrightarrow{G_nA}+$
$\overrightarrow{G_nB}$，所以$\overrightarrow{G_nB}=-\overrightarrow{G_nA}+2\overrightarrow{G_nE}$.又D，$G_n$，B三点共线，
所以$\overrightarrow{G_nD}=\lambda\overrightarrow{G_nB}=-\lambda\overrightarrow{G_nA}+2\lambda\overrightarrow{G_nE}$.又$\overrightarrow{G_nD}=a_{n+1}·$
$\overrightarrow{G_nA}-2(2a_n+3)·\overrightarrow{G_nE}$，所以$\begin{cases}-\lambda=a_{n+1}\\2\lambda=-2(2a_n+3)\end{cases}$，
得$a_{n+1}=2a_n+3$，所以$a_{n+1}+3=2(a_n+3)$，所以数列
$\{a_n+3\}$是等比数列.又$a_1=1$，所以$a_n+3=(a_1+3)2^{n-1}$，
所以$a_n=2^{n+1}-3$.所以$a_3=13$，所以$S_n=\frac{4(1-2^n)}{1-2}=$
$2^{n+2}-3n-4$.故选AB.

8. [2024·桂林中学月考]各项互不相等的等比数列$\{ a_{n}\} $满足$a_{5}· a_{7}=a_{m}· a_{n}$,则$\frac {1}{m}+\frac {4}{n}$的最小值为$\frac{3}{4}$.

答案： 8.$\frac{3}{4}$【解析】由题意知$m+n=5+7=12$，即$\frac{m}{12}+\frac{n}{12}=1(m,$
$n\in N^*)$，则$\frac{1}{m}+\frac{4}{n}=(\frac{1}{m}+\frac{4}{n})·(\frac{m}{12}+\frac{n}{12})=\frac{5}{12}+\frac{n}{12m}+$
$\frac{4m}{12n}\geq\frac{5}{12}+2\sqrt{\frac{n}{12m}·\frac{4m}{12n}}=\frac{3}{4}$，当且仅当$4m^2=n^2$时，等号
成立，此时$m=4$，$n=8$，所以$\frac{1}{m}+\frac{4}{n}$的最小值为$\frac{3}{4}$.