《2026年优选课堂必刷题高一物理全一册人教版》

3. (多选)如下图所示，在灭火抢险的过程中，消防队员有时要借助消防车上的梯子爬到高处进行救人或灭火作业。为了节省救援时间，在消防车向前前进的过程中，人同时相对梯子匀速向上运动，在地面上看消防队员的运动，下列说法中正确的是（ ）

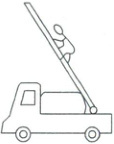
A.当消防车匀速前进时，消防队员一定做匀加速直线运动
B.当消防车匀速前进时，消防队员一定做匀速直线运动
C.当消防车匀加速前进时，消防队员一定做匀变速曲线运动
D.当消防车匀加速前进时，消防队员一定做匀变速直线运动

答案： 3.BC　当消防车匀速前进时，因人同时相对梯子匀速向上运动，根据运动的合成可知，消防队员一定做匀速直线运动，故A错误，B正确；当消防车匀加速前进时，合速度的方向与合加速度的方向不在同一直线上，其加速度的方向大小不变，所以消防员做匀变速曲线运动，故C正确，D错误。

4. (2024·安徽省马鞍山市高一期末)在无风的天气中，雨滴在空中竖直匀速下落，人打伞以一定的速度水平向右匀速运动。如果希望雨垂直打在伞的上表面上（伞面视为平面，伞面可以自动调整方向，伞柄始终处于竖直方向）而少淋雨，下列图中大致正确的打伞方式是（ ）

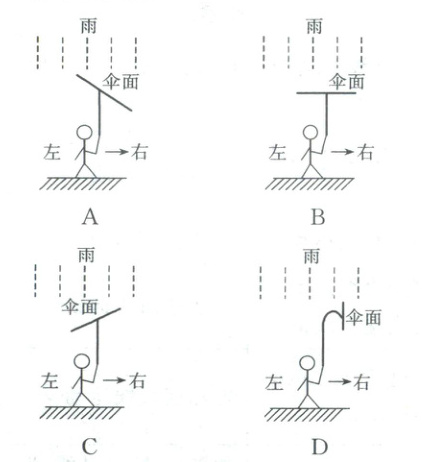
答案：
4.A　由题意可知，雨滴匀速竖直下落，则雨相对于地面的速度$v_{雨地}$向下，人打伞匀速向右急行，即伞相对于地面的速度$v_{伞地}$向右，则地面相对于伞的速度$v_{地伞}$向左，根据矢量的合成可知$v_{雨伞}=v_{雨地}+v_{地伞}$结合平行四边形定则，可知雨滴相对雨伞的速度方向斜向左下，则如果希望雨垂直打在伞的上表面上，雨伞伞面应该像图A一样倾斜。

故A正确，B、C、D错误。

5. (多选)如下图甲所示，在杂技表演中，猴子沿竖直杆向上运动，其$v-t$图像如图乙所示，同时人顶着杆沿水平地面运动的$x-t$图像如图丙所示，若以地面为参考系，下列说法正确的是（ ）


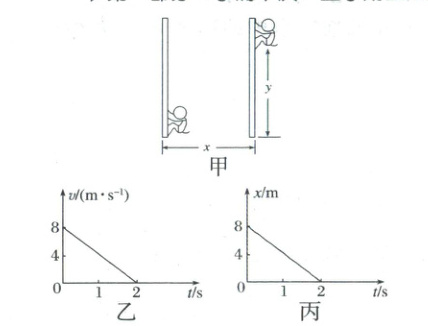
A.猴子的运动轨迹为直线
B.猴子在$0\sim 2s$内做匀变速曲线运动
C.$t=0$时猴子的速度大小为$8m/s$
D.猴子在$0\sim 2s$内的加速度大小为$4m/s^{2}$

答案： 5.BD　猴子在竖直方向做初速度为$8 m/s$、加速度大小为$4 m/s^2$的匀减速直线运动，水平方向做速度大小为$4 m/s$的匀速直线运动，其合运动为曲线运动，故猴子在$0 s \sim 2 s$内做匀变速曲线运动，加速度大小为$4 m/s^2$，选项A错误，B、D正确；$t=0$时猴子的速度大小为$v_0 = \sqrt{v_{0x}^2 + v_{0y}^2} = \sqrt{4^2 + 8^2} m/s = 4\sqrt{5} m/s$，选项C错误。

6. (2024·山东省实验中学高一期中)某次英雄小伙子救人的过程，可用下图去描述：落水孩童抓住绳索停在$A$处，对面河岸上的小伙子从$B$处沿直线匀速游到$A$处，成功把人救起。河宽和间距如图中标注，假定河水在各处的流速均为$2m/s$，则（ ）


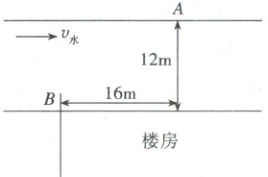
A.小伙子如果面对垂直于河岸的方向游，是不可能到达$A$点的
B.小伙子渡河的时间为$8s$
C.小伙子在静水中游泳的速度至少应为$1.2m/s$，才能成功把人救起
D.只有小伙子总面对着$A$处游，才可能把人救起

答案：
6.C　小伙子的运动可以看成是游泳的运动和他随水流运动的合运动，设小伙子在静水中的游泳的速度为$v_1$，小伙子的合运动方向是从$B$到$A$，作出小伙子游泳时合速度与两个分速度的关系，如图所示：

当$v_1$与合速度垂直时$v_1$有最小值，设$AB$与河岸的夹角为$\theta$，根据几何关系有$\sin \theta = \frac{12}{\sqrt{12^2 + 16^2}} = 0.6$解得$\theta = 37°$，即游泳时小伙子面对的方向是与合速度方向垂直，此时最小的速度为$v_1 = v_{水} \sin \theta = 2 × 0.6 m/s = 1.2 m/s$，故C正确；小伙子如果面对垂直于河岸的方向游，当相对于静水的速度$v_1 = v_{水} \tan 37° = 2 × 0.75 m/s = 1.5 m/s$，恰好到达$A$点，故A错误；只有小伙子在静水中速度垂直于河岸时，小伙子渡河的时间最小，最小的时间为$t = \frac{16}{2} s = 8 s$，小伙子在静水中的速度不与河岸垂直时，小伙子渡河的时间不等于$8 s$，故B错误；若小伙子总面对着$A$处游，且速度一定时，由于两个匀速直线运动的合运动仍然为匀速直线运动，可知，其轨迹为一条直线，根据运动的合成可知，此时其合速度方向指向$A$点右侧，即到达不了$A$处，故D错误。

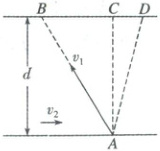
7. 如图所示，河宽$d=120m$，设小船在静水中的速度为$v_{1}$，河水的流速为$v_{2}$，小船从$A$点出发，若船头指向河对岸上游的$B$点，经过$10min$，小船恰好到达河正对岸的$C$点；若船头指向河正对岸的$C$点，经过$8min$，小船到达$C$点下游的$D$点，求：

(1) 小船在静水中的速度$v_{1}$的大小；
(2) 河水的流速$v_{2}$的大小；
(3) 在第二次渡河中小船被冲向下游的距离$s_{CD}$。

答案： 7.解析：
(1)小船从$A$点出发，若船头指向河正对岸的$C$点，则此时$v_1$方向的位移为$d$，
故有$v_1 = \frac{d}{t_{\min}} = \frac{120}{60 × 8} m/s = 0.25 m/s$。
(2)设$AB$与河岸上游成$\alpha$角，由题意可知，此时恰好到达河正对岸的$C$点，故$v_1$沿河岸方向的分速度大小恰好等于河水的流速$v_2$的大小，即$v_2 = v_1 \cos \alpha$，此时渡河时间为$t = \frac{d}{v_1 \sin \alpha}$，所以$\sin \alpha = \frac{d}{v_1 t} = 0.8$，故$v_2 = v_1 \cos \alpha = 0.15 m/s$。
(3)在第二次渡河中小船被冲向下游的距离为$s_{CD} = v_2 t_{\min} = 72 m$。
答案：
(1)$0.25 m/s$　
(2)$0.15 m/s$　
(3)$72 m$