《2026年优选课堂必刷题高一物理全一册人教版》

3. (2025·天津市南开区高一期末)刀、斧，凿等切割工具的刃部叫做劈。如图是斧头劈木头的示意图，劈的纵截面 $ ABC $ 是一个等腰三角形，使用劈时沿 $ BC $ 中垂面施加一个竖直向下的力 $ F $，这个力产生两个作用效果，使劈的两个侧面推压木柴，把木柴劈开。设劈背 $ BC $ 的宽度为 $ d $，劈的侧面 $ AB $、$ AC $ 长为 $ L $，劈的侧面推压木柴的力为 $ F' $，不计劈自身重力，则（ ）


A.劈的侧面推压木柴的力 $ F' = \dfrac{L}{2d}F $
B.仅增大 $ d $；$ F' $ 将增大
C.当 $ d = L $ 时，$ F' = F $
D.仅减小 $ L $，$ F' $ 将增大

答案：
3.C　设劈的纵截面的三角形顶角为$\theta$，根据几何关系可得$\sin\frac{\theta}{2} = \frac{d}{L} = \frac{d}{2L}$，将力$F$按垂直侧面方向进行分解，如图所示：
　　　　　
可得$F_1 = F_2 = \frac{\frac{F}{2}}{\sin\frac{\theta}{2}} = \frac{L}{d}\frac{F}{2}$，则劈的侧面推压木柴的力大小为$F' = F_1 = \frac{L}{d}F$，可知仅增大$d$，$F'$将减小，仅减小$L$，$F'$将减小，当$d = L$时，$F' = F$，故C正确，A、B、D错误。

4. 如下图所示，被轻绳系住静止在光滑斜面上的小球，若按力的实际作用效果来分解小球受到的重力 $ G $，则 $ G $ 的两个分力的方向分别是图中的（ ）


A.$ 1 $ 和 $ 4 $
B.$ 3 $ 和 $ 4 $
C.$ 2 $ 和 $ 4 $
D.$ 3 $ 和 $ 2 $

答案： 4.B　小球的重力产生两个效果，一是使绳子拉伸，二是使斜面受压，故应按这两个方向分解，分别是3和4，故B正确，A、C、D错误。

5. (2024·河北卷，5)如图，弹簧测力计下端挂有一质量为 $ 0.20\ kg $ 的光滑均匀球体，球体静止于带有固定挡板的斜面上，斜面倾角为 $ 30^{\circ} $，挡板与斜面夹角为 $ 60^{\circ} $。若弹簧测力计位于竖直方向，读数为 $ 1.0\ N $，$ g $ 取 $ 10\ m/s^2 $，挡板对球体支持力的大小为（ ）


A.$ \dfrac{\sqrt{3}}{3}\ N $
B.$ 1.0\ N $
C.$ \dfrac{2\sqrt{3}}{3}\ N $
D.$ 2.0\ N $

答案：
5.A　对小球受力分析如图所示：
　　　　　
由几何关系易得力$F$与力$F_N$与竖直方向的夹角均为$30^{\circ}$，因此由正交分解方程可得$F_N\sin30^{\circ} = F\sin30^{\circ}$，$F_N\cos30^{\circ} + F\cos30^{\circ} + F_T = mg$。
解得$F = F_N = \frac{\sqrt{3}}{3}$

6. 如图所示，光滑斜面的倾角为 $ \theta $，有两个相同的小球，分别用光滑挡板 $ A $、$ B $ 挡住，挡板 $ A $ 沿竖直方向，挡板 $ B $ 垂直斜面。试求：

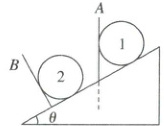
(1)两挡板受到小球压力大小之比。
(2)斜面受到两小球压力大小之比。

答案：
6.解析：球1重力分解如下图甲所示，
　　　　　 　
$F_1 = G\tan\theta,F_2 = \frac{G}{\cos\theta}$
球2重力的分解如图乙所示，$F_1' = G\sin\theta,F_2' = G\cos\theta$
所以挡板A、B所受压力之比$\frac{F_1}{F_1'} = \frac{G\tan\theta}{G\sin\theta} = \frac{1}{\cos\theta}$
斜面所受两小球压力之比$\frac{F_2}{F_2'} = \frac{\frac{G}{\cos\theta}}{G\cos\theta} = \frac{1}{\cos^2\theta}$
答案：
(1)$\frac{1}{\cos\theta}$　
(2)$\frac{1}{\cos^2\theta}$