《2025年新课程助学丛书物理九年级全一册人教版》

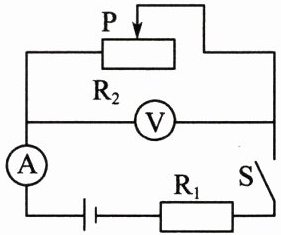
26.（8 分）在下图所示的电路中，$ R_1 = 6\ \Omega $，滑动变阻器的规格为“$ 20\ \Omega\ \ 1\ A $”，电源电压为 $ 4.5\ V $ 且保持不变。电流表的测量范围为 $ 0 \sim 0.6\ A $，电压表的测量范围为 $ 0 \sim 3\ V $。
（1）为保护电表，滑动变阻器接入电路中的阻值范围为多少？
（2）当滑动变阻器接入电路中的阻值 $ R_2 $ 为 $ 9\ \Omega $ 时，电流表、电压表的示数分别为多少？

答案： 26.
(1)$1.5 \sim 12\Omega$　
(2)0.3A　2.7V
解析:由电路图可知，电阻$R_1$和滑动变阻器$R_2$串联，电流表测电路中的电流，电压表测滑动变阻器两端的电压。
(1)当电路中的电流最大时，滑动变阻器接入电路中的电阻最小，若滑动变阻器接入电路中的电阻为0时，则电路中的电流
$I = \frac{U}{R_1} = \frac{4.5V}{6\Omega} = 0.75A$
电流表的测量范围为$0 \sim 0.6A$，滑动变阻器允许通过的最大电流为1A，
所以电路中的最大电流$I_{max} = 0.6A$，
此时电路中的总电阻
$R = \frac{U}{I_{max}} = \frac{4.5V}{0.6A} = 7.5\Omega$
串联电路的总电阻等于各分电阻之和，滑动变阻器接入电路中的最小阻值
$R_{2min} = R - R_1 = 7.5\Omega - 6\Omega = 1.5\Omega$
由串联电路的分压特点可知，滑动变阻器两端的电压最大即$U_{2max} = 3V$时，滑动变阻器接入电路的电阻最大，
根据串联电路的规律和欧姆定律有，$\frac{U_{2max}}{R_{2max}} = \frac{U - U_{2max}}{R_1}$，即$\frac{3V}{R_{2max}} = \frac{4.5V - 3V}{6\Omega}$，
解得$R_{2max} = 12\Omega$，
故滑动变阻器的变化范围为$1.5 \sim 12\Omega$。
(2)当滑动变阻器$R_2$接入电路中的阻值为$9\Omega$时，由电阻的串联和欧姆定律，电路中的电流
$I' = \frac{U}{R_1 + R_2} = \frac{4.5V}{6\Omega + 9\Omega} = 0.3A$，即电流表的示数为0.3A，
滑动变阻器两端的电压
$U_2 = I'R_2 = 0.3A×9\Omega = 2.7V$

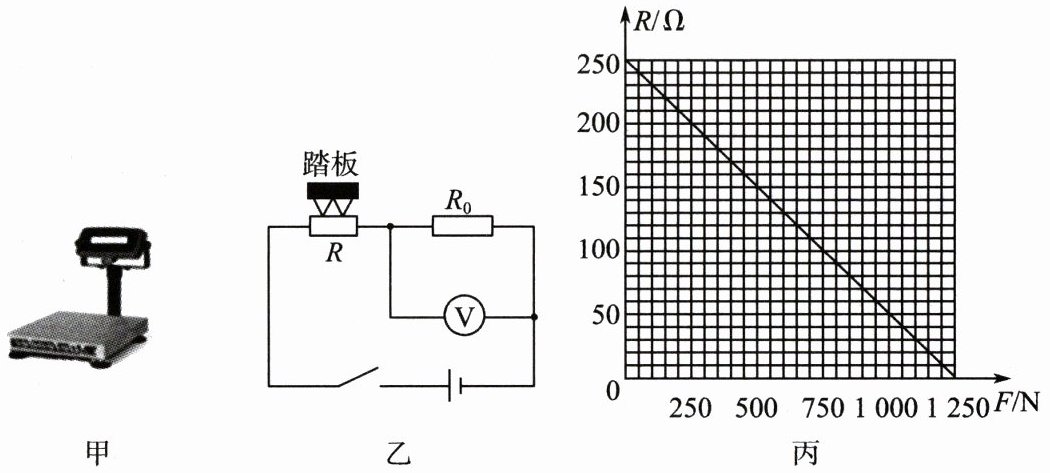
27.（13 分）（2025·江苏扬州模拟）图甲为某型号电子秤，其原理结构如图乙所示；$ R_0 $ 为定值电阻，$ R $ 是压敏电阻，其阻值随所受压力 $ F $ 变化的关系图像如图丙所示；改写电压表（测量范围为 $ 0 \sim 3\ V $）的表盘数值后可直接读出所称量物体的质量；踏板的质量忽略不计，电源电压保持 $ 6\ V $ 不变，$ g $ 取 $ 10\ N/kg $。

（1）空载时，电压表的示数为 $ 1\ V $，求定值电阻 $ R_0 $ 的阻值。
（2）当压力 $ F = 500\ N $ 时，求电压表的示数。
（3）在保证电路安全的情况下，求电子秤的示数变化范围。

答案： 27.
(1)$50\Omega$　
(2)1.5V　
(3)$0 \sim 100kg$
解析:
(1)空载时压敏电阻所受压力为0，由题图丙可知，压敏电阻的阻值$R = 250\Omega$，
根据串联电路中总电压等于各分电压之和可知
$U_R = U - U_0 = 6V - 1V = 5V$
由于串联电路中各处的电流相等，则根据欧姆定律可得，电路中的电流
$I_1 = \frac{U_R}{R} = \frac{5V}{250\Omega} = 0.02A$
$R_0$的阻值$R_0 = \frac{U_0}{I_1} = \frac{1V}{0.02A} = 50\Omega$。
(2)由题图丙知，当压力$F = 500N$时，压敏电阻$R' = 150\Omega$
由串联电路的电阻特点知，电路的总电阻
$R_{总} = R' + R_0 = 150\Omega + 50\Omega = 200\Omega$
根据欧姆定律可得，电路中的电流
$I' = \frac{U}{R_{总}} = \frac{6V}{200\Omega} = 0.03A$
则电压表的示数$U_0 = I'R_0 = 0.03A×50\Omega = 1.5V$
(3)①由
(1)知，空载时电路安全，压敏电阻所受压力为0，电子秤示数最小，$m_{小} = 0kg$；
②已知电压表测量范围为$0 \sim 3V$，则当定值电阻$R_0$两端的电压最大为3V，$R$两端的电压最小，$R$的阻值最小，
根据欧姆定律可知电路中的电流最大，为
$I_{大} = \frac{U_{0大}}{R_0} = \frac{3V}{50\Omega} = 0.06A$
根据串联电路中总电压等于各分电压之和可知
$U_{R小} = U - U_{0大} = 6V - 3V = 3V$
则$R_{小} = \frac{U_{R小}}{I_{大}} = \frac{3V}{0.06A} = 50\Omega$
由题图丙可知，此时压敏电阻受到的压力$F = 1000N$
则所称物体的最大重力为$G = F = 1000N$
则电子秤示数最大为
$m_{大} = \frac{G}{g} = \frac{1000N}{10N/kg} = 100kg$
所以电子秤的示数变化范围为$0 \sim 100kg$。