《2025年课堂精练八年级数学上册北师大版四川专版》

7. 一个三位数,各数位上的数字和为$14$,个位数字与十位数字之和比百位数字大$2$。如果把百位数字与十位数字对调,所得新数比原数小$270$,求原来的三位数。

答案： 解:设原来三位数的个位数字、十位数字、百位数字分别为x,y,z。由题意得$\left\{\begin{array}{l} x+y+z=14,\\ x+y=z+2,\\ 100z+10y+x-270=100y+10z+x,\end{array}\right. $解得$\left\{\begin{array}{l} x=5,\\ y=3,\\ z=6,\end{array}\right. $所以原来的三位数为635。

8. 已知关于$x$,$y的二元一次方程组\begin{cases}2x + 3y = n,\\3x + 5y = n + 2\end{cases} 的解x$,$y的和为12$,则$n$的值为14。

答案： 14

9. 符号$□$,$\triangle$,$◯$各代表一个数字,且满足以下三个等式：$□ + □ + \triangle + ◯ = 17$,$□ + \triangle + \triangle + ◯ = 14$,$□ + \triangle + ◯ + ◯ = 13$,则$□$代表的数字是6。

答案： 6

10. 已知关于$x$,$y的二元一次方程组\begin{cases}2x + 3y = 4,\\kx + (k - 1)y = k - 2\end{cases} 的解x和y$互为相反数,求$k$的值。

答案： 解:因为x和y互为相反数，所以把$x=-y$代入方程$2x+3y=4$得$y=4,$则$x=-4$。把$x=-4,y=4$代入方程$kx+(k-1)y=k-2$得$k=-2$。

11. 【数学应用】某物流公司有$360$箱货物需要运送,现有甲、乙、丙三种车型供运输选择,各种车型每辆车的运载量和运费如下表所示。(假设每辆车均满载)

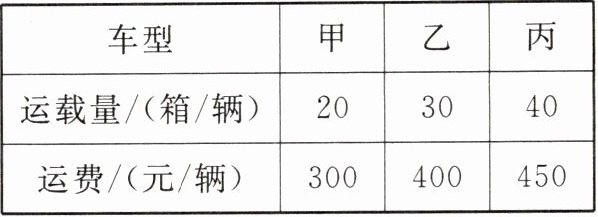
(1)一次性运送全部货物可用甲型车$6$辆,乙型车$4$辆,丙型车3辆；
(2)若全部货物仅用甲、乙两种车型的车一次性运完,需运费$5100$元,求甲、乙两种车型的车各需多少辆；
(3)若该公司打算用甲、乙、丙三种车型的车同时参与运送,已知车总数为$11$辆,且一次性运完所有货物,请设计出所有的运送方案,并写出最少运费。

答案： 解:
(1)3
(2)设甲型车需x辆,乙型车需y辆。根据题意得$\left\{\begin{array}{l} 20x+30y=360,\\ 300x+400y=5100,\end{array}\right. $解得$\left\{\begin{array}{l} x=9,\\ y=6,\end{array}\right. $所以甲型车需9辆,乙型车需6辆。
(3)设使用a辆甲型车,b辆乙型车,c辆丙型车。根据题意得$\left\{\begin{array}{l} a+b+c=11,\\ 20a+30b+40c=360,\end{array}\right. $所以$b=8-2a$,则$c=11-a-b=a+3$。又因为a,b,c均为正整数,所以$\left\{\begin{array}{l} a=1,\\ b=6,\\ c=4\end{array}\right. $或$\left\{\begin{array}{l} a=2,\\ b=4,\\ c=5\end{array}\right. $或$\left\{\begin{array}{l} a=3,\\ b=2,\\ c=6,\end{array}\right. $所以共有3种运送方案。方案1:使用1辆甲型车,6辆乙型车,4辆丙型车；方案2:使用2辆甲型车,4辆乙型车,5辆丙型车；方案3:使用3辆甲型车,2辆乙型车,6辆丙型车。方案1所需运费为$300×1+400×6+450×4=4500$(元);方案2所需运费为$300×2+400×4+450×5=4450$(元);方案3所需运费为$300×3+400×2+450×6=4400$(元)。因为$4500＞4450＞4400,$所以最少运费是4400元。