《2025年课堂精练八年级数学上册北师大版四川专版》

7. 给出下列各式：①$\sqrt{32}$；②$6$；③$\sqrt{-12}$；④$\sqrt{-m}$($m\leq0$)；⑤$\sqrt{a^2 + 1}$；⑥$\sqrt[3]{5}$。其中二次根式的个数是(B)。
A.$2$
B.$3$
C.$4$
D.$5$

答案： B

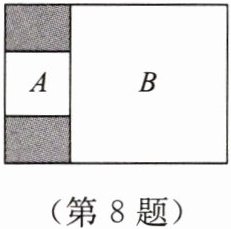
8. 【数学应用】如图,将长方形分成四个区域,其中$A$,$B两正方形区域的面积分别是1和6$,则剩余区域的面积是$\sqrt{6}-1$。

答案： $\sqrt{6}-1$ 分析:因为A,B两正方形区域的面积分别是1和6，
所以A,B两正方形的边长分别是1和$\sqrt{6}$，
故剩余区域的面积是
$\sqrt{6}×(\sqrt{6}+1)-1-6$
$=6+\sqrt{6}-7$
$=\sqrt{6}-1$。

9. 已知$x = \sqrt{6}-\sqrt{2}$,$y = \sqrt{6}+\sqrt{2}$,求$x^2 + 3xy + y^2$的值。

答案： 9.解:因为$x=\sqrt{6}-\sqrt{2},y=\sqrt{6}+\sqrt{2}$，
所以$x^{2}+3xy+y^{2}$
$=(x+y)^{2}+xy$
$=(\sqrt{6}-\sqrt{2}+\sqrt{6}+\sqrt{2})^{2}+(\sqrt{6}-\sqrt{2})×(\sqrt{6}+\sqrt{2})$
$=24+6-2$
$=28$。

10. 若$3 - \sqrt{2}的整数部分为a$,小数部分为$b$,求代数式$b(2 + \sqrt{2}a)$的值。

答案： 10.解:因为$1＜\sqrt{2}＜2$，
所以$1＜3-\sqrt{2}＜2$。
因为$3-\sqrt{2}$的整数部分为$a$,小数部分为$b$，
所以$a=1,b=3-\sqrt{2}-1=2-\sqrt{2}$，
所以$b(2+\sqrt{2}a)=(2-\sqrt{2})×(2+\sqrt{2})=2$。

11. 【综合与实践】观察下列各式：
$\sqrt{1+\frac{1}{1^2}+\frac{1}{2^2}} = 1+\frac{1}{1×2},$
$\sqrt{1+\frac{1}{2^2}+\frac{1}{3^2}} = 1+\frac{1}{2×3},$
$\sqrt{1+\frac{1}{3^2}+\frac{1}{4^2}} = 1+\frac{1}{3×4},$
…请利用你所发现的规律,计算：$\sqrt{1+\frac{1}{1^2}+\frac{1}{2^2}}+\sqrt{1+\frac{1}{2^2}+\frac{1}{3^2}}+\sqrt{1+\frac{1}{3^2}+\frac{1}{4^2}}+…+\sqrt{1+\frac{1}{9^2}+\frac{1}{10^2}}。$

答案： 11.解:由题意可得$\sqrt{1+\dfrac{1}{1^{2}}+\dfrac{1}{2^{2}}}+\sqrt{1+\dfrac{1}{2^{2}}+\dfrac{1}{3^{2}}}+\sqrt{1+\dfrac{1}{3^{2}}+\dfrac{1}{4^{2}}}+\cdots+\sqrt{1+\dfrac{1}{9^{2}}+\dfrac{1}{10^{2}}}$
$=1+\dfrac{1}{1×2}+1+\dfrac{1}{2×3}+1+\dfrac{1}{3×4}+\cdots+1+\dfrac{1}{9×10}$
$=9+\left(1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{4}+\cdots+\dfrac{1}{9}-\dfrac{1}{10}\right)$
$=9+\dfrac{9}{10}$
$=9\dfrac{9}{10}$。