《2025年课堂精练八年级数学上册北师大版四川专版》

8. 给出下列几组数：①$4$,$5$,$6$；②$8$,$15$,$16$；③$n^2 - 1$,$2n$,$n^2 + 1$；④$m^2 - n^2$,$2mn$,$m^2 + n^2$($m＞n＞0$)。其中一定能作为直角三角形三边长的是④。(填序号)

答案： ④

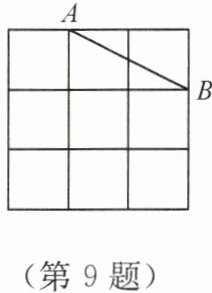
9. 如图,方格中的点$A$,$B$称为格点(格线的交点),以$AB为一边画\triangle ABC$,其中是直角三角形的格点$C$的个数是4。

答案： 4

10. 如图,在$\triangle ABC$中,$AB = 4$,$AC = 3$,$BC = 5$,$AD是\triangle ABC$的角平分线,$DE\perp AB于点E$,求$DE$的长。

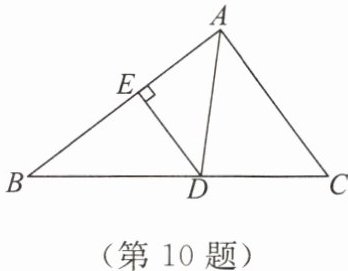
答案： $\frac{12}{7}$

11. 【综合与实践】我们学习了勾股定理后,都知道“勾三、股四、弦五”。
观察：$3$,$4$,$5$；$5$,$12$,$13$；$7$,$24$,$25$；$9$,$40$,$41$；…$$。发现这些勾股数的勾都是奇数,且从$3$起就没有间断过。
(1)请你根据上述规律写出下一组勾股数：11,60,61；
(2)如果第一个数用字母$n$($n$为奇数,且$n\geqslant3$)表示,那么后两个数用含$n$的代数式分别表示为$\frac{n^{2}-1}{2}$和$\frac{n^{2}+1}{2}$,请用所学知识说明它们是一组勾股数。
因为$n^{2}+(\frac{n^{2}-1}{2})^{2}=n^{2}+\frac{n^{4}-2n^{2}+1}{4}=\frac{n^{4}+2n^{2}+1}{4}$,$(\frac{n^{2}+1}{2})^{2}=\frac{n^{4}+2n^{2}+1}{4}$,所以$n^{2}+(\frac{n^{2}-1}{2})^{2}=(\frac{n^{2}+1}{2})^{2}$。又因为n为奇数,且$n\geq3$,所以n,$\frac{n^{2}-1}{2}$,$\frac{n^{2}+1}{2}$是一组勾股数。

答案： 解:
(1)11,60,61
(2)$\frac{n^{2}-1}{2}$ $\frac{n^{2}+1}{2}$因为$n^{2}+(\frac{n^{2}-1}{2})^{2}=n^{2}+\frac{n^{4}-2n^{2}+1}{4}=\frac{n^{4}+2n^{2}+1}{4}$,$(\frac{n^{2}+1}{2})^{2}=\frac{n^{4}+2n^{2}+1}{4}$,所以$n^{2}+(\frac{n^{2}-1}{2})^{2}=(\frac{n^{2}+1}{2})^{2}$。又因为n为奇数,且$n\geq3$,所以n,$\frac{n^{2}-1}{2}$,$\frac{n^{2}+1}{2}$是一组勾股数。

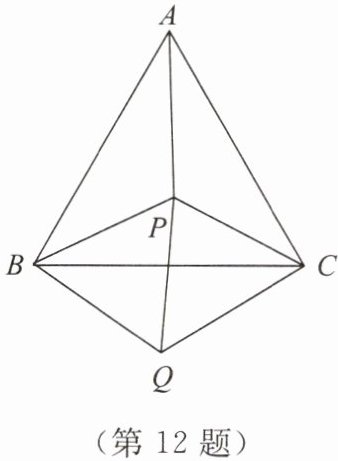
12. 【综合与实践】如图,$P是等边三角形ABC$内的一点,连接$PA$,$PB$,$PC$,以$BP为边作\angle PBQ = 60^{\circ}$,且$BQ = BP$,连接$CQ$。
(1)观察并猜想$AP与CQ$之间的数量关系,并说明理由；
(2)若$PA:PB:PC = 3:4:5$,连接$PQ$,试判断$\triangle PQC$的形状,并说明理由。

答案： 解:
(1)$AP=CQ$。理由如下:因为$\angle ABP+\angle PBC=60^{\circ}$,$\angle CBQ+\angle PBC=60^{\circ}$,所以$\angle ABP=\angle CBQ$。在$\triangle ABP$和$\triangle CBQ$中,$\left\{\begin{array}{l}AB=CB,\\\angle ABP=\angle CBQ,\\BP=BQ,\end{array}\right.$所以$\triangle ABP\cong\triangle CBQ(SAS)$,所以$AP=CQ$。
(2)$\triangle PQC$是直角三角形。理由如下:由$PA:PB:PC=3:4:5$,可设$PA=3a$,$PB=4a$,$PC=5a$。在$\triangle PBQ$中,由于$PB=BQ=4a$,且$\angle PBQ=60^{\circ}$,所以$\triangle PBQ$为等边三角形,所以$PQ=4a$。在$\triangle PQC$中,因为$PQ^{2}+QC^{2}=16a^{2}+9a^{2}=25a^{2}=PC^{2}$,所以$\triangle PQC$是直角三角形。