《2025年课堂精练八年级数学上册北师大版四川专版》

8. 计算：
(1)$4\sqrt{5}+\sqrt{45}-\sqrt{8}+4\sqrt{2}$；
(2)$\sqrt{7}-\sqrt{7}×(7-\sqrt{7})$；
(3)$(1+\sqrt{3})×(3-\sqrt{3})$；
(4)$(\sqrt{\frac{5}{3}}+\sqrt{\frac{3}{5}})×\sqrt{20}$。

答案： 8.解:
(1)原式$=4 \sqrt{5}+3 \sqrt{5}-2 \sqrt{2}+4 \sqrt{2}=7 \sqrt{5}+2 \sqrt{2}$。
(2)原式$=\sqrt{7}-7 \sqrt{7}+7=7-6 \sqrt{7}$。
(3)原式$=3+3 \sqrt{3}-\sqrt{3}-3=2 \sqrt{3}$。
(4)原式$=\sqrt{\frac{5}{3}} × \sqrt{20}+\sqrt{\frac{3}{5}} × \sqrt{20}=\sqrt{\frac{100}{3}}+\sqrt{12}=\frac{10 \sqrt{3}}{3}+2 \sqrt{3}=\frac{16 \sqrt{3}}{3}$。

9. 【综合与实践】小明同学在学习的过程中,遇到这样一道题目：如图,两个正方形的边长分别是多少？你能借助这个图形解释$\sqrt{8}= 2\sqrt{2}$吗？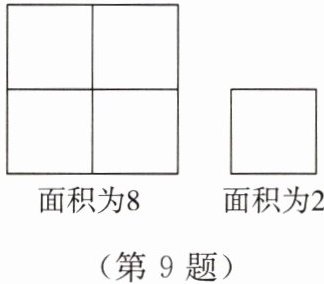
小明想了想做出如下解答过程：“如图,大正方形的面积为$8$,则它的边长为$\sqrt{8}$；小正方形的面积为$2$,则它的边长为$\sqrt{2}$。借助这个图形可以知道大正方形的边长是小正方形边长的$2$倍,即$\sqrt{8}= 2\sqrt{2}$。”
老师夸赞小明做得非常好,为小明提出了一个新的问题：你能设计一个图形解释$\sqrt{\frac{1}{2}}= \frac{\sqrt{2}}{2}$吗？
请你画出相应的图形并借助图形帮助小明解答这个问题。

答案：
9.解:如图,大正方形的面积为2,则它的边长为$\sqrt{2}$;小正方形的面积为$\frac{1}{2}$,则它的边长为$\sqrt{\frac{1}{2}}$。借助这个图形可以知道大正方形的边长是小正方形边长的2倍,即$\sqrt{\frac{1}{2}}=\frac{\sqrt{2}}{2}$。

10. 【综合与实践】在初、高中阶段,要求二次根式化简的最终结果中分母不含有根号,也就是说当分母中有无理数时,要将其化为有理数,实现分母有理化。比如：
(1)$\frac{2}{\sqrt{3}}= \frac{2×\sqrt{3}}{\sqrt{3}×\sqrt{3}}= \frac{2\sqrt{3}}{3}$；
(2)$\frac{2}{\sqrt{3}+1}= \frac{2×(\sqrt{3}-1)}{(\sqrt{3}+1)×(\sqrt{3}-1)}= \frac{2×(\sqrt{3}-1)}{2}= \sqrt{3}-1$。
将下列各式化简：
(1)$\frac{1}{\sqrt{2}}$；
(2)$\frac{1}{\sqrt{2}+1}$；
(3)$\frac{1}{1+\sqrt{2}}+\frac{1}{\sqrt{2}+\sqrt{3}}+…+\frac{1}{\sqrt{8}+\sqrt{9}}$。

答案： 10.解:
(1)$\frac{1}{\sqrt{2}}=\frac{1 × \sqrt{2}}{\sqrt{2} × \sqrt{2}}=\frac{\sqrt{2}}{2}$。
(2)$\frac{1}{\sqrt{2}+1}=\frac{\sqrt{2}-1}{(\sqrt{2}+1) ×(\sqrt{2}-1)}=\sqrt{2}-1$。
(3)因为$\frac{1}{1+\sqrt{2}}=\frac{\sqrt{2}-1}{(1+\sqrt{2}) ×(\sqrt{2}-1)}=\frac{\sqrt{2}-1}{2-1}=\sqrt{2}-1$,$\frac{1}{\sqrt{2}+\sqrt{3}}=\frac{\sqrt{3}-\sqrt{2}}{(\sqrt{2}+\sqrt{3}) ×(\sqrt{3}-\sqrt{2})}=\frac{\sqrt{3}-\sqrt{2}}{3-2}=\sqrt{3}-\sqrt{2}$,$\cdots$$\frac{1}{\sqrt{8}+\sqrt{9}}=\frac{\sqrt{9}-\sqrt{8}}{(\sqrt{8}+\sqrt{9}) ×(\sqrt{9}-\sqrt{8})}=\frac{\sqrt{9}-\sqrt{8}}{9-8}=\sqrt{9}-\sqrt{8}$,所以原式$=(\sqrt{2}-1)+(\sqrt{3}-\sqrt{2})+\cdots+(\sqrt{9}-\sqrt{8})=\sqrt{2}-1+\sqrt{3}-\sqrt{2}+\cdots+\sqrt{9}-\sqrt{8}=\sqrt{9}-1=3-1=2$。