《2025年课堂精练八年级数学上册北师大版四川专版》

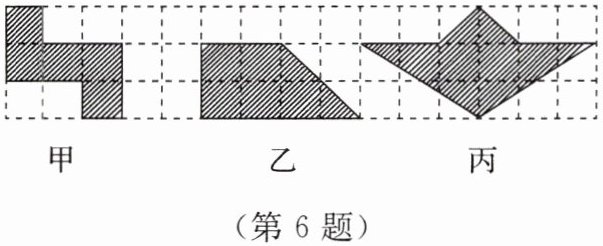
6. 如图所示的是由边长为 1 的小正方形组成的网格。
(1)把图中各阴影部分分别剪拼成大正方形,这些大正方形的面积相等吗？请说明理由。
(2)剪拼成的大正方形的边长是有理数吗？请说明理由。
]

答案： 解:
(1)不相等。
理由如下:如题图甲,阴影部分的面积为5;
如题图乙,阴影部分的面积为$\frac{1}{2}$×(2 + 4)×2 = 6;
如题图丙,阴影部分的面积为$\frac{1}{2}$×6×2 + $\frac{1}{2}$×2×1 = 7。
故这些大正方形的面积不相等。
(2)剪拼成的大正方形的边长都不是有理数。理由如下:设大正方形的边长为x。
如题图甲,阴影部分的面积为5,则大正方形的面积为5,即x² = 5;
如题图乙,阴影部分的面积为6,则大正方形的面积为6,即x² = 6;
如题图丙,阴影部分的面积为7,则大正方形的面积为7,即x² = 7。
综上所述,所有剪拼成的大正方形的边长既不是整数,也不是分数,即都不是有理数。

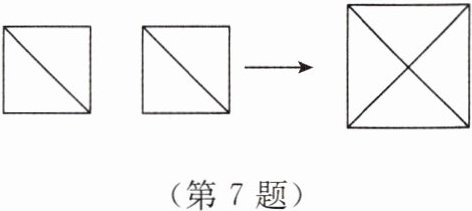
7. 【数学应用】小华家新买了一张边长为 1.4 m 的正方形桌子,原有的边长是 1 m 的两块正方形台布都不适用了,但扔掉太可惜,小华想了一个办法,如图,将两块台布拼成一块正方形大台布。请你帮小华计算一下,这块大台布能盖住新桌子吗？大台布的边长是我们以前学过的有理数吗？为什么？
]

答案： 解:设拼成的大台布的边长为x m。
根据题意,得x² = 2。
因为1.4² = 1.96 ＜ 2,
所以这块大台布能盖住新桌子。
大台布的边长不是我们以前学过的有理数。因为找不到一个整数的平方是2,也找不到一个分数的平方是2,所以它既不是整数,也不是分数,即它不是有理数。

8. 【综合与实践】在以前的学习中,我们已经知道,整数和分数统称有理数。整数可看作分母为 1 的分数或者是小数点后是 0 的小数；分数都可以化成有限小数或者无限循环小数的形式。反过来,任何有限小数和无限循环小数也都可以化成分数的形式。因此,有理数都能化成分数。比如：
①5 可以看作$\frac{5}{1}$。
②$2.4= \frac{24}{10}= \frac{12}{5}$。
③要把$0.\dot{3}$转化成分数形式,可以采用下面的方法：
设$x = 0.\dot{3}= 0.333 3...$,①
则$10x = 3.333 3...$,②
由②－①,得$9x = 3$,解得$x = \frac{1}{3}$,
所以$0.\dot{3}= 0.333 3...= \frac{1}{3}$。
通过阅读以上材料,请你回答下列问题：
(1)整数和分数统称有理数。有理数的表现形式有整数、分数、有限小数、无限循环小数,它们都能化成分数的形式。
(2)把$0.\dot{7}$化成分数。
解:设x = 0.$\dot{7}$ = 0.777…,①
则10x = 7.777…,②
由② - ①,得9x = 7,解得x = $\frac{7}{9}$,
所以0.$\dot{7}$ = 0.777… = $\frac{7}{9}$。

答案： 解:
(1)整数 分数 整数、分数、有限小数、无限循环小数 分数
(2)设x = 0.$\dot{7}$ = 0.777…,①
则10x = 7.777…,②
由② - ①,得9x = 7,解得x = $\frac{7}{9}$,
所以0.$\dot{7}$ = 0.777… = $\frac{7}{9}$。