第8页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
在实际生产、生活中,常会碰到判断两条直线是否垂直的问题,即判断这两条直线构成的角是不是
直角
,若身边没有测量直角的工具,可以构造三角形,通过测量三边的长度,利用勾股定理的逆定理(如果三角形三条边的长度a,b,c满足$a^{2}+b^{2}=c^{2}$,那么这个三角形是直角三角形)
来判断这个三角形是不是直角三角形,从而判断该角是不是直角。
答案:
直角 勾股定理的逆定理(如果三角形三条边的长度a,b,c满足$a^{2}+b^{2}=c^{2}$,那么这个三角形是直角三角形)
1. 如图,由于台风的影响,一棵树在离地面6m处折断,树顶落在离树干底部8m处,则这棵树在折断前(不包括树根)的高度是(
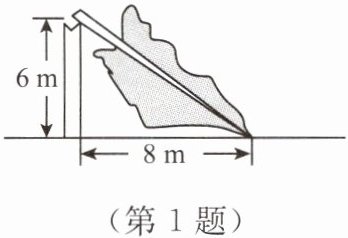
A.8m
B.10m
C.16m
D.18m
C
)。
A.8m
B.10m
C.16m
D.18m
答案:
C
2. 如图,小亮将升旗的绳子拉到旗杆底端,绳子末端刚好接触地面,然后将绳子末端拉到距离旗杆8m处,发现此时绳子末端距离地面2m,则旗杆的高度(滑轮上方的部分忽略不计)为(
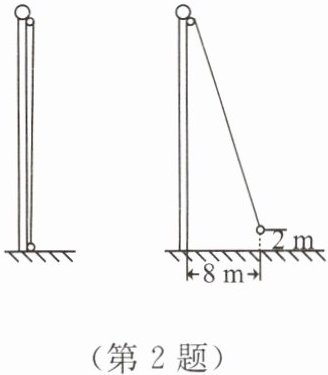
A.12m
B.13m
C.16m
D.17m
D
)。
A.12m
B.13m
C.16m
D.17m
答案:
D
3. 【数学应用】四川省彭州市的九尺镇是著名的大棚蔬菜之乡,常年种植大棚苦瓜、黄瓜、番茄、西葫芦等,秋冬季的蔬菜以莴笋为主。彭州莴笋作为当地特产,已成为四川“大地蔬菜”的代表。如图,彭州市某种植基地为研究新型的蔬菜栽培技术,需要建一个宽3.2m、高2.4m、长15m的蔬菜大棚,则覆盖在顶上的塑料薄膜(图中阴影部分)需要

60m²
。
答案:
$60m^{2}$
4. 如图,有一块四边形空地ABCD,现计划在这块空地上种植草皮。测得AB= 3m,BC= 4m,DA= 13m,CD= 12m,且∠ABC= 90°。若种植每平方米草皮需要200元,则这块空地种植草皮共需要

7200
元。
答案:
7200
5. 如图,在长方形纸片ABCD中,AB= 3,BC= 4,现将点A,C重合,使纸片折叠压平,折痕为EF,求重叠部分△AEF的面积。


答案:
解:由折叠的性质可知$\angle AEF=\angle CEF$,$AE=CE$。
由平行线的性质可知$\angle CEF=\angle AFE$,
所以$\angle AEF=\angle AFE$,
所以$AE=AF=CE$。
设$AE=AF=CE=x$,
则$BE=4 - x$。
在$Rt\triangle ABE$中,
由勾股定理得$AB^{2}+BE^{2}=AE^{2}$,
即$3^{2}+(4 - x)^{2}=x^{2}$,
解得$x=\frac{25}{8}$,
所以$S_{\triangle AEF}=\frac{1}{2}× AF× AB=\frac{1}{2}× \frac{25}{8}× 3=\frac{75}{16}$。
由平行线的性质可知$\angle CEF=\angle AFE$,
所以$\angle AEF=\angle AFE$,
所以$AE=AF=CE$。
设$AE=AF=CE=x$,
则$BE=4 - x$。
在$Rt\triangle ABE$中,
由勾股定理得$AB^{2}+BE^{2}=AE^{2}$,
即$3^{2}+(4 - x)^{2}=x^{2}$,
解得$x=\frac{25}{8}$,
所以$S_{\triangle AEF}=\frac{1}{2}× AF× AB=\frac{1}{2}× \frac{25}{8}× 3=\frac{75}{16}$。
查看更多完整答案,请扫码查看


