《2025年能力素养与学力提升七年级数学上册人教版》

10. 已知$3x^{2} - 4xy + 7y^{2} = 2m - 17$,$x^{2} + 5xy + 6y^{2} = m + 12$,则$\frac{1}{2}x^{2} - 7xy - \frac{5}{2}y^{2}$的值为(B)

A.$-41$
B.$-\frac{41}{2}$
C.$-\frac{9}{2}$
D.$\frac{9}{2}$

答案： B

11. 度数为$82^{\circ}30'16''$的角的补角的度数为97°29'44''.

答案： 97°29'44''

12. $-x^{2m}y^{3}$和$9x^{m + 1}y^{n - 1}$是同类项,则$m - n =$-3.

答案： -3

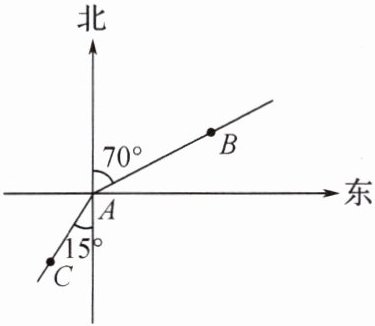
13. 如图,已知甲从点 A 出发向北偏东$70^{\circ}$方向走到点 B,乙从点 A 出发向南偏西$15^{\circ}$方向走到点 C,则$∠BAC$的度数是125°.

答案： 125°

14. 已知多项式$A = ay - 1$,$B = 3ay - 5y - 1$,且多项式$2A + B$中不含字母 y,则 a 的值为1.

答案： 1

15. 按一定规律排列的单项式:$x^{3}$,$-x^{5}$,$x^{7}$,$-x^{9}$,$x^{11}$,…第 n 个单项式是(-1)^{n+1}x^{2n+1}.

答案： $(-1)^{n+1}x^{2n+1}$

16. a,b 在数轴上的位置如图所示,化简:$|a + b| - 2|b - a|=$-3a + b.

答案： -3a + b

17. 已知数轴上有 A,B 两个点对应的数分别是 a,b,且满足$|a + 3| + 2(b - 9)^{2} ≤ 0$;若M 是数轴上一个点,且$MA = 2MB$,则点 M 所对应的数是5 或 21.

答案： 5 或 21

18. 如果关于 x 的一元一次方程$\frac{a}{20}x + \frac{b}{11} = 2a + c$的解为$x = 5$,那么关于 x 的一元一次方程$\frac{a}{20}(x + 1) + \frac{b}{11} = \frac{9}{20}a + c$的解为x = -27.

答案： x = -27

19. (6 分)计算:
(1)$|-\frac{7}{9}|÷(\frac{2}{3} - \frac{1}{5}) - \frac{1}{3}×(-4)^{2}$;
(2)$-1^{2022}÷5×[-1 - (-\frac{1}{5})]$.

答案：
(1) $-\frac{11}{3}$
(2) $\frac{4}{25}$

20. (6 分)解方程:
(1)$3x = 3 - 2(x + 3)$;
(2)$3x + \frac{x - 1}{2} = 3 - \frac{2x - 1}{3}$.

答案：
(1) $x = -\frac{3}{5}$
(2) $x = \frac{23}{25}$