9. 平面上不重合的两点确定一条直线,不同三点最多可确定 3 条直线,若平面上不同的 $ n $ 个点最多可确定 28 条直线,则 $ n $ 的值是(
A.6
B.7
C.8
D.9
C
)A.6
B.7
C.8
D.9
答案:
C
10. 如图,有一种电子游戏,电子屏幕上有一条直线,在直线上有 $ A $,$ B $,$ C $,$ D $ 四点,且 $ AB = BC = CD $,点 $ P $ 沿直线 $ l $ 从左向右移动,当出现点 $ P $ 与 $ A $,$ B $,$ C $,$ D $ 四点中的至少两个点距离相等时,就会发出警报,则直线 $ l $ 上会发出警报的点 $ P $ 有(

A.3 个
B.4 个
C.5 个
D.6 个
C
)
A.3 个
B.4 个
C.5 个
D.6 个
答案:
C
11. 如图,棋盘上有黑、白两色棋子若干,若直线 $ l $ 经过 3 枚颜色相同的棋子,则这样的直线共有

3
条.
答案:
3
12. 已知 $ \angle AOB = 75^{\circ} $,在同一平面内作射线 $ OC $,使得 $ \angle AOC = 25^{\circ} $,则 $ \angle COB = $
50°或100°
.
答案:
50°或100°
13. 如图,射线 $ OB $,$ OC $ 为锐角 $ \angle AOD $ 的三等分线,若图中所有锐角度数之和为 $ 200^{\circ} $,则 $ \angle AOD $ 的度数为

60°
.
答案:
60°
14. 已知点 $ A $,$ B $,$ C $ 依次在一条直线上,若 $ BC = \frac{2}{3}AC $,则 $ \frac{BC}{AB} $ 的值是

2
.
答案:
2
15. 如图,$ \angle AOB = 2\angle BOC $,$ OD $ 平分 $ \angle AOC $,且 $ \angle BOD = 20^{\circ} $,则 $ \angle AOC $ 的度数为
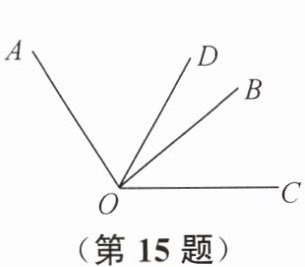
120°
.
答案:
120°
16. 如图,已知 $ \angle AOB = 102^{\circ} $,$ \angle COD = 30^{\circ} $,$ \angle COD $ 在 $ \angle AOB $ 的内部绕点 $ O $ 任意旋转,若 $ OE $ 平分 $ \angle BOC $,则 $ 2\angle AOE + \angle BOD $ 的值为

174°
.
答案:
174°
17. 如图,$ C $ 是线段 $ AB $ 上任意一点(不与端点重合),$ M $ 是 $ AB $ 的中点,$ P $ 是 $ AC $ 的中点,$ Q $ 是 $ BC $ 的中点,则下列说法:① $ PQ = MB $;② $ PM = \frac{1}{2}(AM - MC) $;③ $ PQ = \frac{1}{2}(AQ + AP) $;④ $ MQ = \frac{1}{2}(MB + MC) $. 其中正确的是

①②④
.(填序号)
答案:
①②④
查看更多完整答案,请扫码查看


