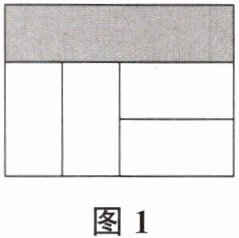
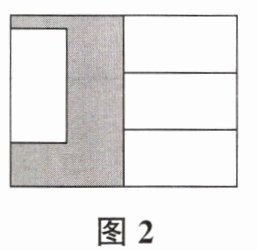
10. 在两个形状、大小完全相同的大长方形内,分别互不重叠地放入四个如图 3 所示的小长方形后得图 1、图 2,已知大长方形的长为$a$,两个大长方形未被覆盖部分分别用阴影表示,则图 1 阴影部分周长与图 2 阴影部分周长的差是(用含$a$的代数式表示)(

A.$-a$
B.$a$
C.$-\frac{1}{2}a$
D.$\frac{1}{2}a$
C
)


A.$-a$
B.$a$
C.$-\frac{1}{2}a$
D.$\frac{1}{2}a$
答案:
C
11. 一个单项式满足下列条件:① 系数是$-\frac{1}{3}$;② 次数是$2$.请写出一个同时满足上述两个条件的单项式:
$-\dfrac{1}{3}ab$
.
答案:
答案不唯一,如$-\dfrac{1}{3}ab$
12. 若多项式$3a + 2b + na + 4$的值与$a$无关,则$n=$
$-3$
.
答案:
$-3$
13. 已知$A = 3a + b$,$B$比$A$小$a - 2b$,$C$比$A$大$2a + b$,则$B=$
$2a+3b$
,$C=$$5a+2b$
.
答案:
$2a+3b$ $5a+2b$
14. 若多项式$ab^{\vert m - n\vert}+(n - 1)a^{3}b^{3}+1$是关于$a$,$b$的五次多项式,则$m$的值为
5或$-3$
.
答案:
5或$-3$
15. 已知关于$x$,$y$的多项式$(a + b)x^{5}+(a - 3)x^{3}-2(b + 2)x^{2}+2ax + 1$不含$x^{3}$和$x^{2}$项,当$x = -1$时,这个多项式的值为
$-6$
.
答案:
$-6$
16. 若$a^{2}+ab = 3$,$ab - b^{2}=6$,则$a^{2}+3ab - 2b^{2}=$
15
.
答案:
15
17. 已知代数式$A = ax^{4}+bx^{3}+cx^{2}+dx + e$.当$x = 2$时,$A$的值为$81$,当$x = -2$时,$A$的值为$1$,则$4b + d$的值为
20
.
答案:
20
18. 定义:若$a + b = n$,则称$a$与$b$是关于$n$的“平衡数”.比如$3$与$-4$是关于$-1$的“平衡数”,$5$与$12$是关于$17$的“平衡数”.现有$a = 6x^{2}-8kx + 12$与$b = -2(3x^{2}-2x + k)$($k$为常数)始终是数$m$的“平衡数”,则$m=$
11
.
答案:
11
19. (10 分)化简:
(1)$2(a - 1)-(2a - 3)$;
(2)$2x^{2}-3x + 4x^{2}-6x - 5$(结果按字母$x$升幂排列);
(3)$(5a^{2}+2a - 1)-2(3 - 8a + 2a^{2})$;
(4)$3x^{2}-\left[5x-\left(\frac{1}{2}x - 3\right)+2x^{2}\right]$;
(5)有理数$a$,$b$,$c$在数轴上的位置如图所示.化简:$3\vert a - b\vert+\vert c + a\vert-2\vert b + c\vert$.

(1)$2(a - 1)-(2a - 3)$;
(2)$2x^{2}-3x + 4x^{2}-6x - 5$(结果按字母$x$升幂排列);
(3)$(5a^{2}+2a - 1)-2(3 - 8a + 2a^{2})$;
(4)$3x^{2}-\left[5x-\left(\frac{1}{2}x - 3\right)+2x^{2}\right]$;
(5)有理数$a$,$b$,$c$在数轴上的位置如图所示.化简:$3\vert a - b\vert+\vert c + a\vert-2\vert b + c\vert$.

答案:
(1)1 (2)$-5-9x+6x^{2}$ (3)$a^{2}+18a-7$ (4)$x^{2}-\dfrac{9}{2}x-3$ (5)$-4a+5b+c$
查看更多完整答案,请扫码查看


