24. (8 分)$A$,$B$,$C$,$D$四个车站的位置如图所示,车站$B$距车站$A$,$D$的距离分别为$(a + b)\mathrm{km}$、$(5a + 3b)\mathrm{km}$,车站$C$与车站$D$的距离为$(3a + 2b)\mathrm{km}$.其中$a$,$b$是不为$0$的实数.
(1)求$B$,$C$两站之间的距离(用含$a$,$b$的代数式表示).
(2)若$B$,$D$两个车站之间的距离比$A$,$B$两个车站之间的距离长$8\mathrm{km}$,求$B$,$C$两个车站相距多少千米.

(1)求$B$,$C$两站之间的距离(用含$a$,$b$的代数式表示).
(2)若$B$,$D$两个车站之间的距离比$A$,$B$两个车站之间的距离长$8\mathrm{km}$,求$B$,$C$两个车站相距多少千米.

答案:
(1)距离为$(5a+3b)-(3a+2b)=5a+3b-3a-2b=2a+b$. $\therefore$ B,C 两站的距离为$(2a+b)\ km$. (2)由题意,得$(5a+3b)-(a+b)=4a+2b=8$,$\therefore 2a+b=4$,即$BC=2a+b=4$.
25. (8 分)【典例展示】若关于$x$,$y$的代数式$ax + 3y - 3x - 2y + 4$的值与$x$无关,求$a$的值.
解:原式$=ax - 3x + 3y - 2y + 4=(a - 3)x + y + 4$.$\because$代数式$ax + 3y - 3x - 2y + 4$的值与$x$无关,$\therefore a - 3 = 0$,$\therefore a = 3$.
【理解应用】已知$A = (4x + 3)(x - 2)-x(1 - 3m)$,$B = x^{2}+mx - 1$,且$A - 4B$的值与$x$无关,求$m$的值;
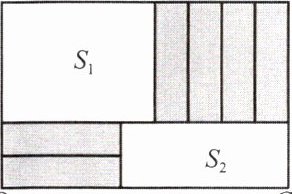
【拓展延伸】用$6$张长为$b$,宽为$a$的长方形纸片按照如图所示的方式不重叠地放在大长方形$ABCD$内,大长方形中未被覆盖的两个部分,设左上角部分的面积为$S_{1}$,右下角部分的面积为$S_{2}$,当$AD$的长度发生变化时,$5S_{2}-2S_{1}$的值始终保持不变,求$a$与$b$之间的数量关系.
解:原式$=ax - 3x + 3y - 2y + 4=(a - 3)x + y + 4$.$\because$代数式$ax + 3y - 3x - 2y + 4$的值与$x$无关,$\therefore a - 3 = 0$,$\therefore a = 3$.
【理解应用】已知$A = (4x + 3)(x - 2)-x(1 - 3m)$,$B = x^{2}+mx - 1$,且$A - 4B$的值与$x$无关,求$m$的值;
【拓展延伸】用$6$张长为$b$,宽为$a$的长方形纸片按照如图所示的方式不重叠地放在大长方形$ABCD$内,大长方形中未被覆盖的两个部分,设左上角部分的面积为$S_{1}$,右下角部分的面积为$S_{2}$,当$AD$的长度发生变化时,$5S_{2}-2S_{1}$的值始终保持不变,求$a$与$b$之间的数量关系.

答案:
【理解应用】$\because A=(4x+3)(x-2)-x(1-3m)=4x^{2}-6x+3mx-6$,$B=x^{2}+mx-1$,$\therefore A-4B=(4x^{2}-6x+3mx-6)-4(x^{2}+mx-1)=4x^{2}-6x+3mx-6-4x^{2}-4mx+4=(-6-m)x-2$. $\because A-4B$的值与$x$无关,$\therefore -6-m=0$,$\therefore m=-6$. (2)设$AD=x$,由图可知$S_{1}=b(x-4a)=bx-4ab$,$S_{2}=2a(x-b)=2ax-2ab$,则$5S_{2}-2S_{1}=5(2ax-2ab)-2(bx-4ab)=10ax-10ab-2bx+8ab=(-2b+10a)x-2ab$. $\because$当$AD$的长度发生变化时,$5S_{2}-2S_{1}$的值始终保持不变,$\therefore 5S_{2}-2S_{1}$的值与$x$的值无关,$\therefore -2b+10a=0$,$\therefore b=5a$.
查看更多完整答案,请扫码查看


