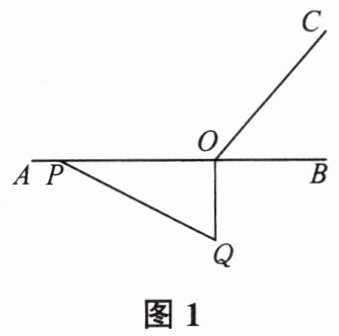
18. 如图 1,$ O $ 为直线 $ AB $ 上一点,作射线 $ OC $,使 $ \angle BOC = 60^{\circ} $,将一个直角三角尺如图摆放,直角顶点在点 $ O $ 处,一条直角边 $ OP $ 在射线 $ OA $ 上. 将图 1 中的三角尺绕点 $ O $ 以每秒 $ 10^{\circ} $ 的速度按逆时针方向旋转(如图 2),在旋转一周的过程中,当 $ t $ 的值为

3或21
时,$ OQ $ 所在直线恰好平分 $ \angle AOC $.

答案:
3或21
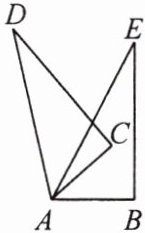
19. (6 分)如图,将两个同样的直角三角尺 $ 60^{\circ} $ 锐角的顶点 $ A $ 重合在一起.
(1)若 $ \angle EAC = 20^{\circ} $,则 $ \angle BAD = $
(2)$ \angle BAD $ 与 $ \angle EAC $ 度数间有怎样的关系?并说明理由.
(1)若 $ \angle EAC = 20^{\circ} $,则 $ \angle BAD = $
100°
;(2)$ \angle BAD $ 与 $ \angle EAC $ 度数间有怎样的关系?并说明理由.

答案:
(1)100° (2)∠BAD+∠EAC=120°.理由如下:由题意,得∠DAC=∠EAB=60°,
∵∠CAB=∠EAB-∠EAC=60°-∠EAC,
∴∠BAD=∠DAC+∠CAB=60°+60°-∠EAC=120°-∠EAC.
∴∠BAD+∠EAC=120°.
∵∠CAB=∠EAB-∠EAC=60°-∠EAC,
∴∠BAD=∠DAC+∠CAB=60°+60°-∠EAC=120°-∠EAC.
∴∠BAD+∠EAC=120°.
20. (6 分)补全解题过程.
如图,$ B $ 是线段 $ AC $ 上一点,且 $ AB = 6 $,$ BC = \frac{1}{3}AB $,$ O $ 是线段 $ AC $ 的中点. 求线段 $ OB $ 的长.

解:$ \because AB = 6 $,$ BC = \frac{1}{3}AB $,$ \therefore BC = \frac{1}{3}AB = $
$ \because AC = AB + BC $,$ \therefore AC = $
$ \because O $ 是线段 $ AC $ 的中点,$ \therefore CO = \frac{1}{2} $
$ \therefore OB = CO - BC = $
如图,$ B $ 是线段 $ AC $ 上一点,且 $ AB = 6 $,$ BC = \frac{1}{3}AB $,$ O $ 是线段 $ AC $ 的中点. 求线段 $ OB $ 的长.

解:$ \because AB = 6 $,$ BC = \frac{1}{3}AB $,$ \therefore BC = \frac{1}{3}AB = $
2
.$ \because AC = AB + BC $,$ \therefore AC = $
8
.$ \because O $ 是线段 $ AC $ 的中点,$ \therefore CO = \frac{1}{2} $
AC
$ = $4
(理由:线段中点的定义
).$ \therefore OB = CO - BC = $
2
.
答案:
2 8 AC 4 线段中点的定义 2
21. (6 分)线段与角的计算.
(1)如图 1,$ C $,$ E $ 是线段 $ AB $ 上的两点. 若 $ AB = 6 $,$ BC = 2 $,且 $ AE : EC = 1 : 3 $,求 $ EC $ 的长;
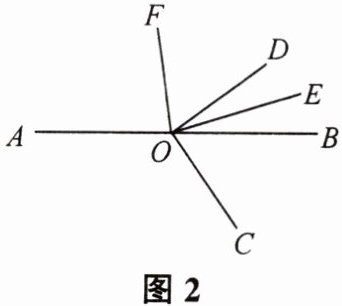
(2)如图 2,$ O $ 为直线 $ AB $ 上一点,且 $ \angle COD $ 为直角,$ OE $ 平分 $ \angle BOD $,$ OF $ 平分 $ \angle AOE $. 若 $ \angle BOC + \angle FOD = 117^{\circ} $,求 $ \angle BOE $ 的度数.


(1)如图 1,$ C $,$ E $ 是线段 $ AB $ 上的两点. 若 $ AB = 6 $,$ BC = 2 $,且 $ AE : EC = 1 : 3 $,求 $ EC $ 的长;
(2)如图 2,$ O $ 为直线 $ AB $ 上一点,且 $ \angle COD $ 为直角,$ OE $ 平分 $ \angle BOD $,$ OF $ 平分 $ \angle AOE $. 若 $ \angle BOC + \angle FOD = 117^{\circ} $,求 $ \angle BOE $ 的度数.



答案:
(1)EC=3 (2)∠BOE的度数是18°.
查看更多完整答案,请扫码查看


