《2025年能力素养与学力提升七年级数学上册人教版》

22. (6 分)如图，点 $ C $ 在线段 $ AB $ 上，图中共有三条线段 $ AB $，$ AC $，$ BC $，若其中有一条线段的长度是另外一条线段长度的 2 倍，则称点 $ C $ 是线段 $ AB $ 的“巧点”.
(1)线段的中点是这条线段的“巧点”；(填“是”或“不是”)
(2)若 $ AB = 12 \, cm $，点 $ C $ 是线段 $ AB $ 的“巧点”，求 $ AC $ 的长.

答案： （1）是 （2）AC的长为4 cm或6 cm或8 cm.

23. （9 分）已知 $ \angle AOB = 120^{\circ} $，$ \angle COD = 90^{\circ} $，$ OE $ 平分 $ \angle AOD $.
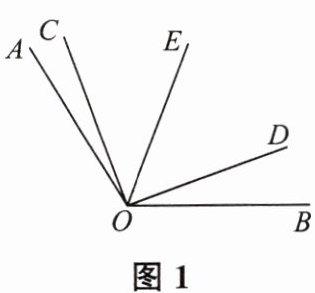
（1）如图 1，当 $ \angle COD $ 的边 $ OD $ 在 $ \angle AOB $ 内部时，若 $ \angle COE = 40^{\circ} $，求 $ \angle BOD $ 的度数；
（2）如图 2，当 $ \angle COD $ 的边 $ OD $ 在 $ \angle AOB $ 外部时，且 $ 0^{\circ} ＜ \angle BOD ＜ 60^{\circ} $ 时，设 $ \angle COE = \alpha $，$ \angle BOD = \beta $，用等式表示 $ \alpha $ 与 $ \beta $ 之间的数量关系，并说明理由.

答案： （1）20° （2）2α+β=60°.理由如下：
∵∠COD=90°，∠COE=α，
∴∠DOE=∠COD-∠COE=90°-α.
∵OE平分∠AOD，
∴∠AOD=2∠DOE=2(90°-α)=180°-2α.
∵∠AOB=120°，
∴∠BOD=β=∠AOD-∠AOB=180°-2α-120°=60°-2α，即2α+β=60°.