第65页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
2. 如图是由一些正方形和直角三角形拼合而成的图形,其中最大正方形的边长为7 cm,则正方形 A,B,C,D 的面积之和为______
49
$.zyjl.cn/pic18/2025-09-04/5b8bd0717a18642b0cea00404644051e.jpg?x-oss-process=image/crop,x_619,y_376,w_278,h_350">$
答案:
49
3. 如图,两个全等的 $ Rt\triangle ADE $,$ Rt\triangle BEC $ 的边 AE,EB 在同一条直线上. 历史上曾有人利用该图形证明了勾股定理,证明中用到的面积相等关系是(
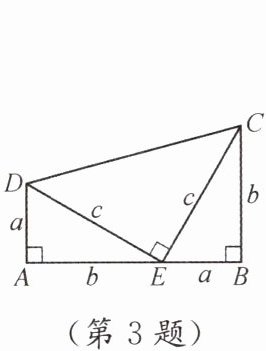
A.$ S_{\triangle EDA}= S_{\triangle CEB} $
B.$ S_{\triangle EDA}+S_{\triangle CEB}= S_{\triangle CDE} $
C.$ S_{四边形C D A E}= S_{四边形C D E B} $
D.$ S_{\triangle EDA}+S_{\triangle CDE}+S_{\triangle CEB}= S_{四边形ABCD} $
D
)
A.$ S_{\triangle EDA}= S_{\triangle CEB} $
B.$ S_{\triangle EDA}+S_{\triangle CEB}= S_{\triangle CDE} $
C.$ S_{四边形C D A E}= S_{四边形C D E B} $
D.$ S_{\triangle EDA}+S_{\triangle CDE}+S_{\triangle CEB}= S_{四边形ABCD} $
答案:
D
1. 如图,小明用 4 个如图①所示的长方形组成图②,其中四边形 ABCD,EFGH,MNPQ 都是正方形. 求证:$ a^{2}+b^{2}= c^{2} $.
 ______
______
 ______
______
答案:
由题意,图①为长$a$、宽$b$、对角线$c$的长方形,4个图①长方形组成图②,其中ABCD、EFGH、MNPQ为正方形。
1. 大正方形ABCD的面积:
其边长为长方形长与宽之和$a + b$,面积$S_{ABCD}=(a + b)^2=a^2 + 2ab + b^2$。
2. 小正方形MNPQ的面积:
大正方形ABCD面积等于4个长方形面积与MNPQ面积之和。4个长方形面积为$4ab$,设MNPQ边长为$d$,则$a^2 + 2ab + b^2=4ab + d^2$,解得$d^2=(a - b)^2$,即$S_{MNPQ}=(a - b)^2$。
3. 正方形EFGH的面积:
EFGH边长为长方形对角线$c$,面积$S_{EFGH}=c^2$。EFGH面积等于MNPQ面积与4个直角三角形(每个长方形含2个,取其中4个)面积之和,每个直角三角形面积$\frac{1}{2}ab$,4个面积为$2ab$。故$c^2=(a - b)^2 + 2ab$。
4. 化简得结论:
展开$(a - b)^2 + 2ab=a^2 - 2ab + b^2 + 2ab=a^2 + b^2$,即$a^2 + b^2=c^2$。
综上,$a^2 + b^2=c^2$得证。
1. 大正方形ABCD的面积:
其边长为长方形长与宽之和$a + b$,面积$S_{ABCD}=(a + b)^2=a^2 + 2ab + b^2$。
2. 小正方形MNPQ的面积:
大正方形ABCD面积等于4个长方形面积与MNPQ面积之和。4个长方形面积为$4ab$,设MNPQ边长为$d$,则$a^2 + 2ab + b^2=4ab + d^2$,解得$d^2=(a - b)^2$,即$S_{MNPQ}=(a - b)^2$。
3. 正方形EFGH的面积:
EFGH边长为长方形对角线$c$,面积$S_{EFGH}=c^2$。EFGH面积等于MNPQ面积与4个直角三角形(每个长方形含2个,取其中4个)面积之和,每个直角三角形面积$\frac{1}{2}ab$,4个面积为$2ab$。故$c^2=(a - b)^2 + 2ab$。
4. 化简得结论:
展开$(a - b)^2 + 2ab=a^2 - 2ab + b^2 + 2ab=a^2 + b^2$,即$a^2 + b^2=c^2$。
综上,$a^2 + b^2=c^2$得证。
2. 2002 年 8 月,国际数学家大会在北京召开,其会标取材于我国古代数学家赵爽的“弦图”,此图是由 4 个的全等直角三角形和 1 个小正方形构成的大正方形. 如图,若 $ AB= c $,大正方形的面积为 13,中间小正方形的面积为 2,且直角三角形的两直角边分别为 a,b,求 $ (a+b)^{2} $ 的值.
 ______
______
 ______
______
答案:
24
查看更多完整答案,请扫码查看


