第59页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
活动一:忆一忆 写一写
1.
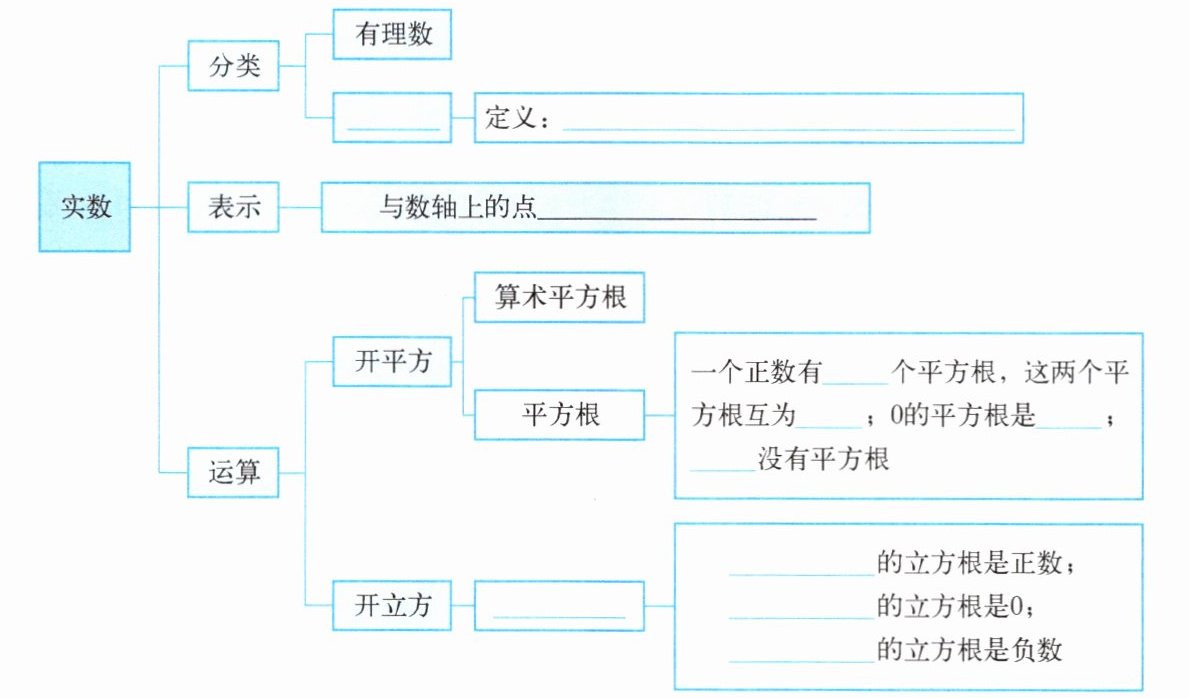
2. 请你分别写出两个无理数与有理数.
3. 说说实数如何分类.
1.

分类:无理数;表示:一一对应;运算:开平方中,一个正数有2个平方根,这两个平方根互为相反数;0的平方根是0;负数没有平方根。开立方中,正数的立方根是正数;0的立方根是0;负数的立方根是负数。
2. 请你分别写出两个无理数与有理数.
两个无理数:$\pi$,$\sqrt{2}$;两个有理数:$2$,$\frac{1}{2}$ 。
3. 说说实数如何分类.
实数分类:按定义分:实数可分为有理数和无理数。有理数是整数(正整数、$0$、负整数)和分数统称;无理数是无限不循环小数。按大小分:实数可分为正实数、$0$、负实数。
答案:
2. 两个无理数:$\pi$,$\sqrt{2}$;两个有理数:$2$,$\frac{1}{2}$ 。
3. 实数分类:
按定义分:实数可分为有理数和无理数。有理数是整数(正整数、$0$、负整数)和分数统称;无理数是无限不循环小数。
按大小分:实数可分为正实数、$0$、负实数。
图中填空:
分类:无理数;
表示:一一对应;
运算:开平方中,一个正数有$2$个平方根,这两个平方根互为相反数;$0$的平方根是$0$;负数没有平方根。开立方中,正数的立方根是正数;$0$的立方根是$0$;负数的立方根是负数。
3. 实数分类:
按定义分:实数可分为有理数和无理数。有理数是整数(正整数、$0$、负整数)和分数统称;无理数是无限不循环小数。
按大小分:实数可分为正实数、$0$、负实数。
图中填空:
分类:无理数;
表示:一一对应;
运算:开平方中,一个正数有$2$个平方根,这两个平方根互为相反数;$0$的平方根是$0$;负数没有平方根。开立方中,正数的立方根是正数;$0$的立方根是$0$;负数的立方根是负数。
活动二:想一想 做一做
1. 我们在学习“实数”时,画了这样一个图,即“以数轴上的单位长度为‘1’的线段画一个正方形,然后以原点为圆心,正方形的对角线长为半径画弧交x轴于点A”.

请根据图2-2,回答下列问题:
(1)线段OA的长是
(2)画这个图形是为了说明什么?
(3)这种研究和解决问题的方式,体现的数学思想方法是(
1. 我们在学习“实数”时,画了这样一个图,即“以数轴上的单位长度为‘1’的线段画一个正方形,然后以原点为圆心,正方形的对角线长为半径画弧交x轴于点A”.

请根据图2-2,回答下列问题:
(1)线段OA的长是
$\sqrt{2}$
.(2)画这个图形是为了说明什么?
画这个图形是为了说明实数与数轴上的点是一一对应的,对于数轴上这个表示$\sqrt{2}$的点A,可以用一个以原点为圆心,正方形对角线为半径的弧与x轴的交点来表示,体现了实数能在数轴上找到对应的点。
(3)这种研究和解决问题的方式,体现的数学思想方法是(
A
)
答案:
(1)
由勾股定理,正方形的边长为$1$,则对角线长$OB = \sqrt{1^{2}+1^{2}}=\sqrt{2}$,因为$OA = OB$,所以线段$OA$的长是$\sqrt{2}$。
(2)
画这个图形是为了说明实数与数轴上的点是一一对应的,对于数轴上这个表示$\sqrt{2}$的点$A$,可以用一个以原点为圆心,正方形对角线为半径的弧与$x$轴的交点来表示,体现了实数能在数轴上找到对应的点。
(3)A
(1)
由勾股定理,正方形的边长为$1$,则对角线长$OB = \sqrt{1^{2}+1^{2}}=\sqrt{2}$,因为$OA = OB$,所以线段$OA$的长是$\sqrt{2}$。
(2)
画这个图形是为了说明实数与数轴上的点是一一对应的,对于数轴上这个表示$\sqrt{2}$的点$A$,可以用一个以原点为圆心,正方形对角线为半径的弧与$x$轴的交点来表示,体现了实数能在数轴上找到对应的点。
(3)A
查看更多完整答案,请扫码查看


