《2025年学能评价六年级数学上册人教版》

1. 填表。

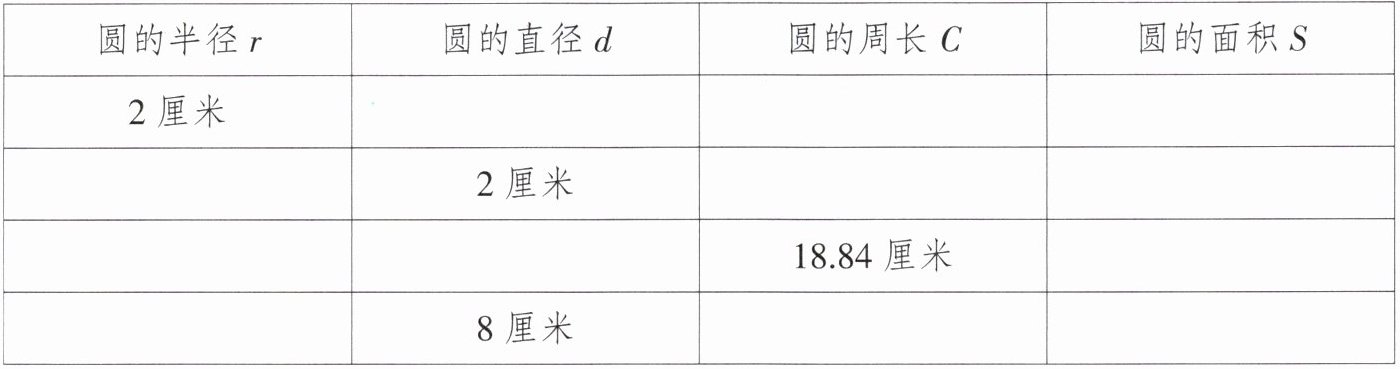
答案： 表格从第一行到第四行依次填：4厘米，12.56厘米，12.56平方厘米；1厘米，6.28厘米，3.14平方厘米；3厘米，6厘米，28.26平方厘米；4厘米，25.12厘米，50.24平方厘米。

2. 将一个圆剪开后拼成一个近似长方形，长方形的周长比圆的周长长 $ 12 $ 厘米，求圆的面积。

答案： 解：将圆剪开拼成近似长方形，长方形的长为圆周长的一半（$\pi r$），宽为圆的半径（$r$）。
长方形周长 = $2(\pi r + r)$，圆的周长 = $2\pi r$。
两者周长差：$2(\pi r + r) - 2\pi r = 2r$。
已知周长差为12厘米，即$2r = 12$，解得$r = 6$厘米。
圆的面积 = $\pi r^2 = 3.14×6^2 = 113.04$平方厘米。
答：圆的面积是113.04平方厘米。

3. 有两个圆，小圆的周长是 $ 15.7 $ 米，大圆的直径是小圆直径的 $ 2 $ 倍，求大圆的面积。

答案： 首先根据圆的周长公式 $C = \pi d$，可以求出小圆的直径 $d$：
$d = \frac{C}{\pi} = \frac{15.7}{3.14} = 5（米）$，
接着，根据题目条件，大圆的直径是小圆直径的2倍，即：
$D = 2d = 2 × 5 = 10（米）$，
然后，可以求出大圆的半径 $R$：
$R = \frac{D}{2} = \frac{10}{2} = 5（米）$，
最后，根据圆的面积公式 $S = \pi R^{2}$，可以求出大圆的面积：
$S = \pi R^{2} = 3.14 × 5^{2} = 78.5（平方米）$。
所以大圆的面积78.5 平方米。

4. 某圆形湖周长 $ 3140 $ 米，在湖的中间有一个面积是 $ 3000 $ 平方米的小岛。如果在湖中种满莲花，每平方米水面可以收莲子 $ 0.05 $ 千克。一共可以收莲子多少千克？

答案： 由圆周长公式$C = 2\pi r$，已知$C = 3140$米，$\pi$取$3.14$，
则$r = C÷(2\pi)=3140÷(2×3.14) = 500$（米）。
那么湖的面积$S=\pi r^{2}=3.14×500^{2}=785000$（平方米）。
因为湖中间有一个面积是$3000$平方米的小岛，
所以种莲花的水面面积为$785000 - 3000 = 782000$（平方米）。
已知每平方米水面可以收莲子$0.05$千克，
则一共可以收莲子$782000×0.05 = 39100$（千克）。
综上，一共可以收莲子$39100$千克。

5. 一只羊被 $ 5 $ 米长的绳子拴在正方形建筑物的一个墙角，正方形边长为 $ 3 $ 米，周围是草地。这只羊能吃到草的草地面积是()平方米。($ \pi $ 取 $ 3 $)

答案： 62.25