《2025年学能评价六年级数学上册人教版》

1. 一辆汽车的车轮外直径是 60 厘米，平均每分钟转 100 转，过一座大桥，用了 15 分钟。这座大桥全长多少米？

答案： 车轮的周长：$C = \pi d = 3.14 × 60 = 188.4$（厘米）。
每分钟汽车行驶的距离：$188.4 × 100 = 18840$（厘米） = 188.4（米）。
大桥的全长：$188.4 × 15 = 2826$（米）。
答：这座大桥的全长为$2826$米。

2. 在一个直径是 30 米的圆形水池周围插上护栏，每隔 3.14 米插一根。一共要插多少根？

答案： 1. 圆形水池直径$d = 30$米，根据圆的周长公式$C=\pi d$，可得周长$C = 3.14×30=94.2$米。
2. 每隔$3.14$米插一根护栏，由于是在圆形上插，根数等于间隔数，所以护栏根数为$94.2÷3.14 = 30$根。
结论：30根

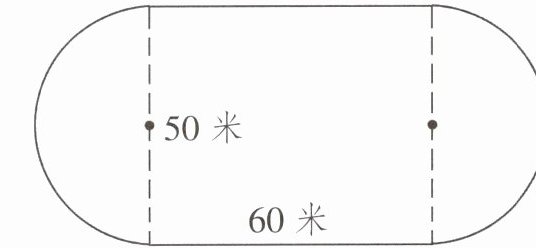
3. 天天绕着学校操场跑了一圈，他一共跑了多少米？

答案： 3. 操场周长=圆的周长+长方形两条长的长度
圆的周长：$C = \pi d = 3.14 × 50 = 157$（米）
长方形两条长：$60 × 2 = 120$（米）
总路程：$157 + 120 = 277$（米）
答：他一共跑了277米。

4. 有一个正方形的水池，它的边长是 10 米，将它改造成一个圆形的鱼塘，但周长不变，那么圆形鱼塘的半径大约是多少米？（结果保留两位小数）

答案： 由题意知，正方形水池的边长为$10$米，
所以，正方形的周长为$4 × 10 = 40$（米），
因为圆形鱼塘的周长与正方形水池的周长相等，
所以圆形鱼塘的周长也为$40$米，
设圆形鱼塘的半径为$r$米，
根据圆的周长公式：$C = 2\pi r$，
有$2\pi r = 40$，
解得$r \approx 6.37$（米），
所以圆形鱼塘的半径大约是$6.37$米。

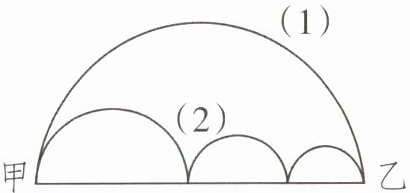
5. 聪聪想从甲地到乙地去，有（1）（2）两条路可走。如果你是聪聪，你会选择哪条路呢？为什么？

答案： 设半圆的直径为$ D$，三个小半圆的直径分别为$d_1, d_2, d_3$，且满足$d_1+d_2+d_3=D$。
路线
(1) 的长度：
路线
(1) 是一个半圆，其半径为$D/2$。
$长度 = \frac{1}{2} × 2\pi × \frac{D}{2} = \pi × \frac{D}{2} = \frac{\pi D}{2}$。
路线
(2) 的长度：
路线
(2) 由三个半圆组成，其半径分别为$d_1/2, d_2/2, d_3/2$。
$总长度 = \frac{1}{2} × 2\pi × \frac{d_1}{2} + \frac{1}{2} × 2\pi × \frac{d_2}{2} + \frac{1}{2} × 2\pi × \frac{d_3}{2} $
$= \pi × \frac{d_1}{2} + \pi × \frac{d_2}{2} + \pi × \frac{d_3}{2}$
$ = \frac{\pi (d_1 + d_2 + d_3)}{2} $
$= \frac{\pi D}{2}$
两条路线的长度相同，因此选择哪条路线都可以。