《2025年学能评价六年级数学上册人教版》

1. 图中大正方形的面积是 40 平方米，求阴影部分的面积。

答案： 设大正方形的边长为$a$，则$a^2 = 40$ 平方米。
大圆的直径等于正方形的边长$a$，所以大圆的半径$r = \frac{a}{2}$。
阴影部分为正方形内去掉大圆后的部分，所以阴影部分的面积为正方形面积减去大圆面积。
大圆面积$S_{圆} = \pi r^2 = \pi \left( \frac{a}{2} \right)^2 = \frac{\pi a^2}{4}$。
阴影部分面积$S_{阴影} = a^2 - \frac{\pi a^2}{4} = 40 - \frac{\pi × 40}{4} = 40 - 10\pi$。
故阴影部分面积为$(40 - 10\pi)$平方米。

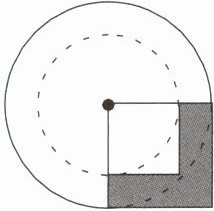
2. 已知阴影部分的面积是 80 平方厘米，那么环形的面积是多少平方厘米？

答案： 设外圆半径为$ R $，内圆半径为$ r $。
阴影部分面积为大正方形面积减去小正方形面积，即$ R^2 - r^2 = 80 \, cm^2 $。
环形面积公式：$ S_{环形} = \pi (R^2 - r^2) $。
代入得：$ S_{环形} = 3.14 × 80 = 251.2 \, cm^2 $。
答：环形的面积是251.2平方厘米。

3. 求下面图形阴影部分的面积。（单位：米）

答案： 136.69平方米（若保留两位小数）或136.6875平方米
（注：若题目中π取值不同，结果可调整，此处按π=3.14计算）

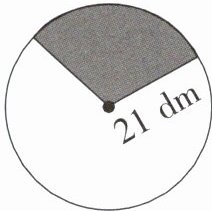
4. 下图中的阴影部分占了圆面积的 $\frac{1}{3}$。求阴影部分的面积。

答案： 解：圆的面积公式为$S = \pi r^2$（其中$r$为半径），已知半径$r = 21dm$，$\pi$取$3.14$。
则圆的面积为$3.14×21^2 = 3.14×441 = 1384.74dm^2$。
因为阴影部分占圆面积的$\frac{1}{3}$，所以阴影部分面积为$1384.74×\frac{1}{3}=461.58dm^2$。
综上，阴影部分的面积是$461.58dm^2$。