2025年一线名师总复习暑假作业海南出版社五年级数学人教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年一线名师总复习暑假作业海南出版社五年级数学人教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
1. 已知除数是37,商是8,当余数取最大值时,被除数是(
332
)。
答案:
解析:本题可根据有余数的除法中余数和除数的关系,先确定余数的最大值,再根据被除数、除数、商和余数的关系求出被除数。
在有余数的除法中,余数一定小于除数,已知除数是$37$,那么余数最大为$36$。
根据被除数$=$商$×$除数$ +$余数,已知商是$8$,除数是$37$,余数是$36$,则被除数为:
$8×37 + 36$
$=296+36$
$=332$
答案:$332$。
在有余数的除法中,余数一定小于除数,已知除数是$37$,那么余数最大为$36$。
根据被除数$=$商$×$除数$ +$余数,已知商是$8$,除数是$37$,余数是$36$,则被除数为:
$8×37 + 36$
$=296+36$
$=332$
答案:$332$。
2. $125×80$的积的末尾一共有(
4
)个0;$160×2$的积的末尾一共有(1
)个0。
答案:
解析:
本题考查的是乘法运算。
首先,计算125×80:
125×80=10000。
末尾一共有4个0。
接着,计算160×2:
160×2=320。
末尾一共有1个0。
答案:
4;1。
本题考查的是乘法运算。
首先,计算125×80:
125×80=10000。
末尾一共有4个0。
接着,计算160×2:
160×2=320。
末尾一共有1个0。
答案:
4;1。
3. 要使$□63÷54$的商是一位数,$□$里最大填(
4
);要使$□34÷47$的商是两位数,$□$里最小填(5
)。
答案:
解析:
第一个问题,要使$□63 ÷ 54$的商是一位数,需要找到一个数字替代$□$,使得$□63$小于$54 × 10 = 540$,因此$□$里应该填的数字要小于$5$(因为$563$已经大于$540$了),所以最大可以填$4$。
第二个问题,要使$□34 ÷ 47$的商是两位数,需要找到一个数字替代$□$,使得$□34$大于等于$47 × 10 = 470$,因此$□$里应该填的数字要大于等于$5$(因为$434$小于$470$),所以最小可以填$5$。
答案:
要使$□63 ÷ 54$的商是一位数,$□$里最大填$4$;
要使$□34 ÷ 47$的商是两位数,$□$里最小填$5$。
第一个问题,要使$□63 ÷ 54$的商是一位数,需要找到一个数字替代$□$,使得$□63$小于$54 × 10 = 540$,因此$□$里应该填的数字要小于$5$(因为$563$已经大于$540$了),所以最大可以填$4$。
第二个问题,要使$□34 ÷ 47$的商是两位数,需要找到一个数字替代$□$,使得$□34$大于等于$47 × 10 = 470$,因此$□$里应该填的数字要大于等于$5$(因为$434$小于$470$),所以最小可以填$5$。
答案:
要使$□63 ÷ 54$的商是一位数,$□$里最大填$4$;
要使$□34 ÷ 47$的商是两位数,$□$里最小填$5$。
4. 两个数相乘,积是160,一个因数不变,另一个因数扩大到原来的10倍,积变为(
1600
)。
答案:
解析:根据积的变化规律,一个因数不变,另一个因数扩大或缩小若干倍(0除外),积就扩大或缩小相同的倍数。
已知两个数相乘积是160,一个因数不变,另一个因数扩大到原来的10倍,那么积也会扩大到原来的10倍,所以积变为$160×10 = 1600$。
答案:1600。
已知两个数相乘积是160,一个因数不变,另一个因数扩大到原来的10倍,那么积也会扩大到原来的10倍,所以积变为$160×10 = 1600$。
答案:1600。
5. 478大约是79的(
6
)倍;104的20倍大约是(2000
)。
答案:
解析:本题可根据倍数关系以及估算的方法来分别计算两个空的答案。
计算$478$大约是$79$的几倍:
求一个数是另一个数的几倍用除法计算,即$478÷79$,题目要求大约的倍数,所以可对$478$和$79$进行估算,把$478$看作$480$,把$79$看作$80$,则$478÷79\approx480÷80 = 6$。
计算$104$的$20$倍大约是多少:
求一个数的几倍是多少用乘法计算,即$104×20$,题目要求大约的结果,所以可对$104$进行估算,把$104$看作$100$,则$104×20\approx100×20 = 2000$。
答案:$6$;$2000$。
计算$478$大约是$79$的几倍:
求一个数是另一个数的几倍用除法计算,即$478÷79$,题目要求大约的倍数,所以可对$478$和$79$进行估算,把$478$看作$480$,把$79$看作$80$,则$478÷79\approx480÷80 = 6$。
计算$104$的$20$倍大约是多少:
求一个数的几倍是多少用乘法计算,即$104×20$,题目要求大约的结果,所以可对$104$进行估算,把$104$看作$100$,则$104×20\approx100×20 = 2000$。
答案:$6$;$2000$。
6. 根据$352÷16= 22$直接写出下面各题的结果。
$352÷32= $
$352÷32= $
11
$1056÷16= $66
答案:
解析:
本题可根据商的变化规律来求解。
对于$352÷32$:
在除法算式中,被除数不变,除数扩大或缩小几倍($0$除外),则商缩小或扩大相同的倍数。
已知$352÷16 = 22$,在$352÷32$中,被除数$352$不变,除数由$16$变为$32$,$32÷16 = 2$,即除数扩大了$2$倍,那么商应缩小$2$倍,所以$352÷32 = 22÷2 = 11$。
对于$1056÷16$:
在除法算式中,除数不变,被除数扩大或缩小几倍($0$除外),则商也随之扩大或缩小相同的倍数。
已知$352÷16 = 22$,在$1056÷16$中,除数$16$不变,被除数由$352$变为$1056$,$1056÷352 = 3$,即被除数扩大了$3$倍,那么商也应扩大$3$倍,所以$1056÷16 = 22×3 = 66$。
答案:
$11$;$66$
本题可根据商的变化规律来求解。
对于$352÷32$:
在除法算式中,被除数不变,除数扩大或缩小几倍($0$除外),则商缩小或扩大相同的倍数。
已知$352÷16 = 22$,在$352÷32$中,被除数$352$不变,除数由$16$变为$32$,$32÷16 = 2$,即除数扩大了$2$倍,那么商应缩小$2$倍,所以$352÷32 = 22÷2 = 11$。
对于$1056÷16$:
在除法算式中,除数不变,被除数扩大或缩小几倍($0$除外),则商也随之扩大或缩小相同的倍数。
已知$352÷16 = 22$,在$1056÷16$中,除数$16$不变,被除数由$352$变为$1056$,$1056÷352 = 3$,即被除数扩大了$3$倍,那么商也应扩大$3$倍,所以$1056÷16 = 22×3 = 66$。
答案:
$11$;$66$
二、判断。(对的打“√”,错的打“×”)
1. 两个因数的乘积一定比这两个因数都大。 (
2. 两位自然数乘两位自然数,积一定是四位自然数。 (
3. 甲数除以乙数的商是26,如果甲数和乙数同时乘2,那么这两个数的商就变成了104。 (
1. 两个因数的乘积一定比这两个因数都大。 (
×
)2. 两位自然数乘两位自然数,积一定是四位自然数。 (
×
)3. 甲数除以乙数的商是26,如果甲数和乙数同时乘2,那么这两个数的商就变成了104。 (
×
)
答案:
解析:
1. 题目考查因数的乘积与因数本身的大小关系。因数的乘积不一定比这两个因数都大,例如其中一个因数为1或0时,乘积不会比两个因数都大,或者两个小数相乘,乘积可能比其中至少一个因数小。
2. 题目考查两位自然数相乘的结果位数。两位自然数乘两位自然数,积不一定是四位自然数,有可能是三位数,例如$10 × 10 = 100$。
3. 题目考查商的变化规律。如果甲数和乙数同时乘一个相同的数,商不会改变,因为乘除同一个数相当于没有改变他们之间的比例。
答案:
1. ×
2. ×
3. ×
1. 题目考查因数的乘积与因数本身的大小关系。因数的乘积不一定比这两个因数都大,例如其中一个因数为1或0时,乘积不会比两个因数都大,或者两个小数相乘,乘积可能比其中至少一个因数小。
2. 题目考查两位自然数相乘的结果位数。两位自然数乘两位自然数,积不一定是四位自然数,有可能是三位数,例如$10 × 10 = 100$。
3. 题目考查商的变化规律。如果甲数和乙数同时乘一个相同的数,商不会改变,因为乘除同一个数相当于没有改变他们之间的比例。
答案:
1. ×
2. ×
3. ×
三、列竖式计算。(除不尽的保留余数,带*的要验算)
$408×40= $ $786×23= $ *$576÷68= $
$9600÷800= $ *$56×320= $ $734÷62= $
$408×40= $ $786×23= $ *$576÷68= $
$9600÷800= $ *$56×320= $ $734÷62= $
答案:
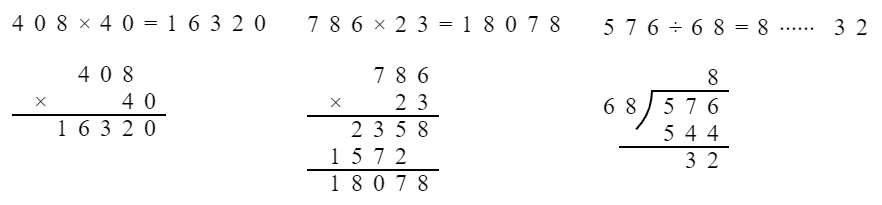
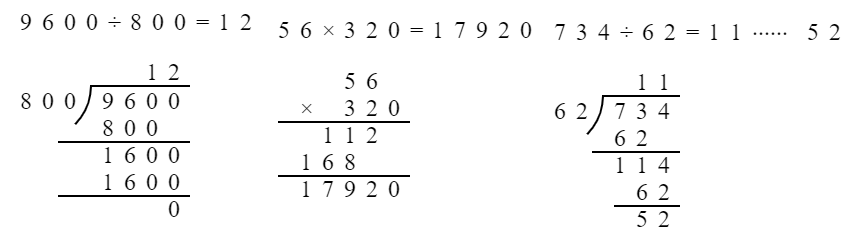
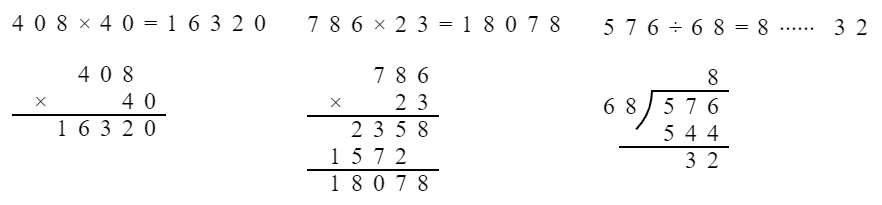
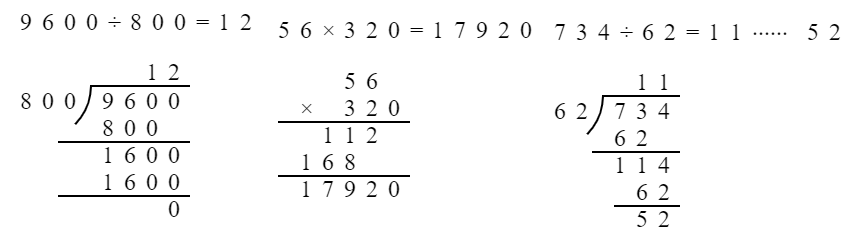
查看更多完整答案,请扫码查看


