《2025年一线名师总复习暑假作业海南出版社五年级数学人教版》

1. 下图中一共有(1)条直线,(8)条射线,(6)条线段。

答案： 1. 首先明确直线、射线、线段的定义：
直线：没有端点，向两方无限延伸的线。
射线：直线上的一点，可向一方无限延伸，有一个端点。
线段：直线上两点间的一段，有两个端点。
2. 然后数直线的数量：
图中只有$1$条直线，因为直线是向两方无限延伸的，整个图形中这样的线只有$1$条。
3. 接着数射线的数量：
因为图中有$4$个点，每个点可以向左、向右各形成一条射线，根据射线的定义，射线的数量为$4×2 = 8$条。
4. 最后数线段的数量：
根据线段的定义，利用组合公式$C_{n}^2=\frac{n(n - 1)}{2}$（$n$为点的个数），这里$n = 4$，则$C_{4}^2=\frac{4×(4 - 1)}{2}=\frac{4×3}{2}=6$条；也可以用列举法：设四个点为$A$、$B$、$C$、$D$，线段有$AB$、$AC$、$AD$、$BC$、$BD$、$CD$共$6$条。
所以答案依次为：$1$；$8$；$6$。

2. 一个等腰直角三角形的底角是(45)度。

答案： 解析：等腰直角三角形有一个$90^\circ$的直角，还有两个相等的底角。
由三角形内角和为$180^\circ$的性质，可以计算出底角的度数。
设底角的度数为$x$，则：
$90^\circ + 2x = 180^\circ$
$2x = 90^\circ$
$x = 45^\circ$
答案：$45$。

3. 一个平行四边形和一个三角形的底和高都相等,平行四边形的面积是三角形的(2)倍。

答案： 设平行四边形和三角形的底为$b$，高为$h$。
平行四边形面积：$S_{\text{平}} = b × h$
三角形面积：$S_{\text{三}} = \frac{1}{2} × b × h$
则$S_{\text{平}} ÷ S_{\text{三}} = (b × h) ÷ (\frac{1}{2} × b × h) = 2$
2

4. 平角的一半是(90)度,是(直)角,是周角的$\frac{(1)}{(4)}$。

答案： 解析：首先，平角是$180^\circ$，它的一半即为$180^\circ ÷ 2 = 90^\circ$。$90^\circ$的角被称为直角。另外，周角是$360^\circ$，因此$90^\circ$是周角的$\frac{90}{360} = \frac{1}{4}$。
答案：$90$，直，$\frac{1}{4}$。

5. 求下面各图中$∠1$的度数。

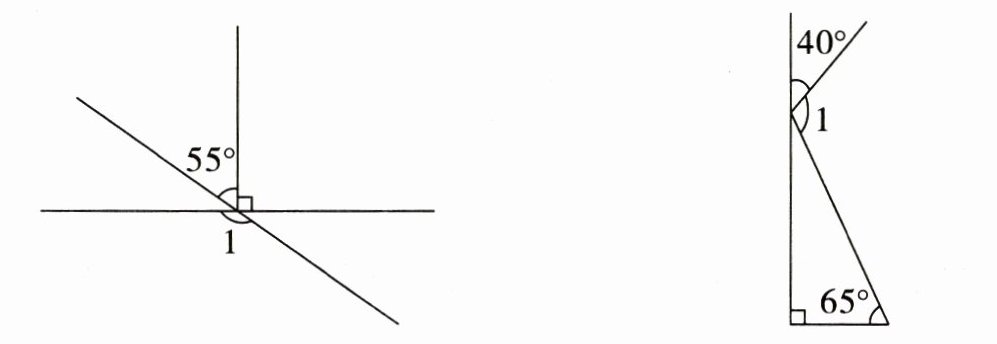
$∠1=$$145^{\circ}$$∠1=$$105^{\circ}$

答案： $∠1=145^{\circ}$
$∠1=105^{\circ}$

二、判断。(对的打“√”,错的打“×”)
1. 同一平面内,不平行的两条直线一定相交。(√)
2. 一条射线长3米。(×)
3. 大于$90^{\circ}$的角是钝角。(×)
4. 把一个长方形拉成一个平行四边形,面积不变。(×)

答案： 解析：
1. 题目考查的是同一平面内两条直线的位置关系。根据几何知识，同一平面内两条直线要么平行，要么相交。因此，该说法是正确的。
答案：√
2. 题目考查的是射线的性质。射线是有一个固定端点，可以无限延伸的直线，因此它没有确定的长度。所以，说一条射线长3米是错误的。
答案：×
3. 题目考查的是角的分类。大于$90^{\circ}$且小于$180^{\circ}$的角是钝角，但大于$180^{\circ}$的角不是钝角。因此，仅仅说大于$90^{\circ}$的角是钝角是不准确的。
答案：×
4. 题目考查的是长方形和平行四边形的面积关系。长方形的面积是长乘以宽，而平行四边形的面积是底乘以高。当长方形被拉成平行四边形时，虽然底（长方形的一边）保持不变，但高（与底垂直的距离）会发生变化，因此面积也会改变。
答案：×

1. 只有一组对边平行的四边形叫做(C)。
A.长方形
B.平行四边形
C.梯形

答案： 解析：本题考查梯形的定义。
A选项：长方形两组对边都平行，不符合“只有一组对边平行”的条件，所以A选项错误。
B选项：平行四边形两组对边都平行，不符合“只有一组对边平行”的条件，所以B选项错误。
C选项：梯形是只有一组对边平行的四边形，符合题意，所以C选项正确。
答案：C。