2025年暑假作业甘肃少年儿童出版社高一物理人教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年暑假作业甘肃少年儿童出版社高一物理人教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
7. 铁道转弯处内、外铁轨间设计有高度差,可以有利于火车顺利转弯,下列说法正确的是(
A.主要是为了减少车轮与铁轨间的摩擦
B.主要是为了减少轮缘与铁轨间的挤压
C.内轨应略高于外轨
D.重力和支持力的合力为火车转弯提供了向心力
BD
)A.主要是为了减少车轮与铁轨间的摩擦
B.主要是为了减少轮缘与铁轨间的挤压
C.内轨应略高于外轨
D.重力和支持力的合力为火车转弯提供了向心力
答案:
解:铁道转弯处外轨高于内轨,目的是使重力和支持力的合力提供向心力,减少轮缘与铁轨间的挤压。
A. 不是为了减少车轮与铁轨间的摩擦,A错误;
B. 主要是为了减少轮缘与铁轨间的挤压,B正确;
C. 外轨应略高于内轨,C错误;
D. 重力和支持力的合力为火车转弯提供了向心力,D正确。
答案:B、D
A. 不是为了减少车轮与铁轨间的摩擦,A错误;
B. 主要是为了减少轮缘与铁轨间的挤压,B正确;
C. 外轨应略高于内轨,C错误;
D. 重力和支持力的合力为火车转弯提供了向心力,D正确。
答案:B、D
8. 如图所示,有一个半径为 $ R $ 的光滑圆轨道,现给小球一个初速度,使小球在竖直面内做圆周运动,则关于小球在过最高点的速度 $ v $,下列叙述中正确的是(
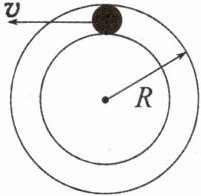
A.$ v $ 的极小值为 $ \sqrt{gR} $
B.$ v $ 由零逐渐增大,轨道对球的弹力逐渐增大
C.当 $ v $ 由 $ \sqrt{gR} $ 值逐渐增大时,轨道对小球的弹力也逐渐增大
D.当 $ v $ 由 $ \sqrt{gR} $ 值逐渐减小时,轨道对小球的弹力逐渐增大
CD
)
A.$ v $ 的极小值为 $ \sqrt{gR} $
B.$ v $ 由零逐渐增大,轨道对球的弹力逐渐增大
C.当 $ v $ 由 $ \sqrt{gR} $ 值逐渐增大时,轨道对小球的弹力也逐渐增大
D.当 $ v $ 由 $ \sqrt{gR} $ 值逐渐减小时,轨道对小球的弹力逐渐增大
答案:
解:小球在最高点时,向心力由重力和轨道弹力提供,设轨道对小球的弹力为 $ N $(方向竖直向下为正),则有:
$ mg + N = m\frac{v^2}{R} $
分析选项:
- A:当 $ N = 0 $ 时,$ v = \sqrt{gR} $,此时为最小速度,若 $ v < \sqrt{gR} $,则 $ N $ 为负值(轨道对小球有竖直向上的支持力),小球仍能通过最高点,故极小值不为 $ \sqrt{gR} $,A 错误。
- B:当 $ v < \sqrt{gR} $ 时,$ N = m\frac{v^2}{R} - mg < 0 $(支持力),$ v $ 增大时,$ |N| $ 减小;当 $ v > \sqrt{gR} $ 时,$ N = m\frac{v^2}{R} - mg > 0 $(压力),$ v $ 增大时,$ N $ 增大,B 错误。
- C:当 $ v > \sqrt{gR} $ 时,$ N = m\frac{v^2}{R} - mg $,$ v $ 增大,$ N $ 增大,C 正确。
- D:当 $ v < \sqrt{gR} $ 时,$ N = mg - m\frac{v^2}{R} $(支持力大小),$ v $ 减小,$ N $ 增大,D 正确。
结论:C、D
$ mg + N = m\frac{v^2}{R} $
分析选项:
- A:当 $ N = 0 $ 时,$ v = \sqrt{gR} $,此时为最小速度,若 $ v < \sqrt{gR} $,则 $ N $ 为负值(轨道对小球有竖直向上的支持力),小球仍能通过最高点,故极小值不为 $ \sqrt{gR} $,A 错误。
- B:当 $ v < \sqrt{gR} $ 时,$ N = m\frac{v^2}{R} - mg < 0 $(支持力),$ v $ 增大时,$ |N| $ 减小;当 $ v > \sqrt{gR} $ 时,$ N = m\frac{v^2}{R} - mg > 0 $(压力),$ v $ 增大时,$ N $ 增大,B 错误。
- C:当 $ v > \sqrt{gR} $ 时,$ N = m\frac{v^2}{R} - mg $,$ v $ 增大,$ N $ 增大,C 正确。
- D:当 $ v < \sqrt{gR} $ 时,$ N = mg - m\frac{v^2}{R} $(支持力大小),$ v $ 减小,$ N $ 增大,D 正确。
结论:C、D
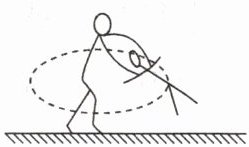
9. (16 分)如图所示是双人花样滑冰运动中男运动员拉着女运动员做圆锥摆运动的精彩场面的简图。若女运动员做圆锥摆运动时和竖直方向的夹角为 $ \theta $,女运动员的质量为 $ m $,转动过程中女运动员的重心做匀速圆周运动的半径为 $ r $,重力加速度为 $ g $,求这时男运动员对女运动员的拉力大小及两人转动的角速度。

答案:
解:女运动员受重力 $ mg $ 和男运动员的拉力 $ F $ 作用,两力的合力提供向心力。
在竖直方向:$ F\cos\theta = mg $,解得拉力 $ F = \frac{mg}{\cos\theta} $。
在水平方向:$ F\sin\theta = m\omega^2 r $,将 $ F = \frac{mg}{\cos\theta} $ 代入得 $ \frac{mg}{\cos\theta} \sin\theta = m\omega^2 r $,化简得 $ g\tan\theta = \omega^2 r $,解得角速度 $ \omega = \sqrt{\frac{g\tan\theta}{r}} $。
男运动员对女运动员的拉力大小为 $ \frac{mg}{\cos\theta} $,两人转动的角速度为 $ \sqrt{\frac{g\tan\theta}{r}} $。
在竖直方向:$ F\cos\theta = mg $,解得拉力 $ F = \frac{mg}{\cos\theta} $。
在水平方向:$ F\sin\theta = m\omega^2 r $,将 $ F = \frac{mg}{\cos\theta} $ 代入得 $ \frac{mg}{\cos\theta} \sin\theta = m\omega^2 r $,化简得 $ g\tan\theta = \omega^2 r $,解得角速度 $ \omega = \sqrt{\frac{g\tan\theta}{r}} $。
男运动员对女运动员的拉力大小为 $ \frac{mg}{\cos\theta} $,两人转动的角速度为 $ \sqrt{\frac{g\tan\theta}{r}} $。
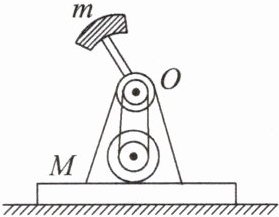
10. (20 分)如图是小型电动打夯机的结构示意图,电动机带动质量为 $ m = 50\ \text{kg} $ 的重锤(重锤可视为质点)绕转轴 $ O $ 匀速运动,重锤转动半径为 $ R = 0.5\ \text{m} $。电动机连同打夯机底座的质量为 $ M = 25\ \text{kg} $,重锤和转轴 $ O $ 之间连接杆的质量可以忽略不计, $ g $ 取 $ 10\ \text{m/s}^2 $。求:
(1)重锤转动的角速度为多大时,才能使打夯机底座刚好离开地面?
(2)若重锤以上述的角速度转动,当打夯机的重锤通过最低位置时,打夯机对地面的压力为多大?
(1)重锤转动的角速度为多大时,才能使打夯机底座刚好离开地面?
(2)若重锤以上述的角速度转动,当打夯机的重锤通过最低位置时,打夯机对地面的压力为多大?

答案:
(1)解:当重锤运动到最高点时,打夯机底座刚好离开地面,此时底座对地面压力为零,连接杆对重锤的拉力 $ F $ 满足 $ F + mg = m\omega^2 R $,且 $ F = Mg $。
联立得 $ Mg + mg = m\omega^2 R $,代入数据 $ M = 25\ \text{kg} $,$ m = 50\ \text{kg} $,$ R = 0.5\ \text{m} $,$ g = 10\ \text{m/s}^2 $:
$ 25×10 + 50×10 = 50×\omega^2×0.5 $
$ 750 = 25\omega^2 $
$ \omega^2 = 30 $
$ \omega = \sqrt{30}\ \text{rad/s} $
(2)解:重锤在最低点时,连接杆对重锤的拉力 $ F' $ 满足 $ F' - mg = m\omega^2 R $,此时打夯机对地面压力 $ N = F' + Mg $。
由
(1)知 $ m\omega^2 R = 750\ \text{N} $,则 $ F' = mg + 750 = 50×10 + 750 = 1250\ \text{N} $
$ N = 1250 + 25×10 = 1500\ \text{N} $
答案:
(1) $ \sqrt{30}\ \text{rad/s} $;
(2) $ 1500\ \text{N} $
(1)解:当重锤运动到最高点时,打夯机底座刚好离开地面,此时底座对地面压力为零,连接杆对重锤的拉力 $ F $ 满足 $ F + mg = m\omega^2 R $,且 $ F = Mg $。
联立得 $ Mg + mg = m\omega^2 R $,代入数据 $ M = 25\ \text{kg} $,$ m = 50\ \text{kg} $,$ R = 0.5\ \text{m} $,$ g = 10\ \text{m/s}^2 $:
$ 25×10 + 50×10 = 50×\omega^2×0.5 $
$ 750 = 25\omega^2 $
$ \omega^2 = 30 $
$ \omega = \sqrt{30}\ \text{rad/s} $
(2)解:重锤在最低点时,连接杆对重锤的拉力 $ F' $ 满足 $ F' - mg = m\omega^2 R $,此时打夯机对地面压力 $ N = F' + Mg $。
由
(1)知 $ m\omega^2 R = 750\ \text{N} $,则 $ F' = mg + 750 = 50×10 + 750 = 1250\ \text{N} $
$ N = 1250 + 25×10 = 1500\ \text{N} $
答案:
(1) $ \sqrt{30}\ \text{rad/s} $;
(2) $ 1500\ \text{N} $
查看更多完整答案,请扫码查看


