《2025年暑假作业甘肃少年儿童出版社高一物理人教版》

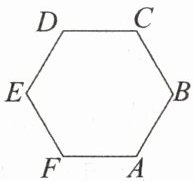
8. 如图所示,A、B、C、D、E、F 为匀强电场中一个边长为 1 m 的正六边形的六个顶点,A、B、C 三点电势分别为 10 V、20 V、30 V,则下列说法正确的是(AD)

A.B、E 一定处在同一等势面上
B.匀强电场的场强大小为 10 V/m
C.正点电荷从 E 点移到 F 点,则电场力做负功
D.电子从 F 点移到 D 点,电荷的电势能减少 20 eV

答案： 解：
1. 等势面分析：
正六边形中，A(10V)、B(20V)、C(30V)电势沿AB、BC方向均匀升高，故AB、BC为匀强电场中沿场强垂直方向的等势线的垂线。连接A、C，AC中点电势为20V，与B点电势相等，故B在AC中垂线上。根据正六边形对称性，E点与B点关于中心对称，电势相等（均为20V），则B、E在同一等势面，A正确。
2. 场强大小计算：
A、B两点沿场强方向距离为 $ d = AB \cdot \cos60^\circ = 1 \, \text{m} × 0.5 = 0.5 \, \text{m} $，电势差 $ U_{BA} = 10 \, \text{V} $，场强 $ E = \frac{U}{d} = \frac{10}{0.5} = 20 \, \text{V/m} $，B错误。
3. 电场力做功判断：
由对称性，F点电势10V，E点电势20V，正电荷从E(20V)移到F(10V)，电势能降低，电场力做正功，C错误。
4. 电势能变化：
D点电势30V，F点电势10V，电子从F移到D，电势差 $ U_{FD} = 20 \, \text{V} $，电场力做功 $ W = -eU_{FD} = -20 \, \text{eV} $，电势能减少20eV，D正确。
结论：A、D正确。
答案：AD

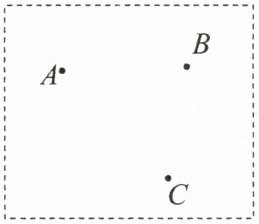
9. (16 分)如图,虚线方框内有一匀强电场,A、B、C 为该电场中的三点,已知：$ \varphi_A = 12V $,$ \varphi_B = 6V $,$ \varphi_C = -6V $。试在该虚线框内作出该电场的示意图(画出几条电场线),并要求保留作图时所用的辅助线。

答案：
【解析】要画电场线，先找等势线。因为$U_{AC}=18V$、$U_{AB}=6V$、$\frac{U_{AC}}{U_{AB}} = 3$，将线段$AC$等分成三份，使$AH = HF = FC$，则$φ_{H}=6V$，$φ_{F}=0$，故$B$、$H$电势相等。连接$BH$即为等势线，由电场线与等势线垂直且由高电势指向低电势，可画出电场线如图所示。

答案:见解析图

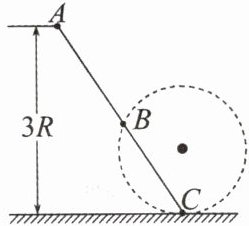
10. (20 分)如图所示,在竖直平面内,光滑绝缘直杆 AC 与半径为 R 的圆周交于 B、C 两点,在圆心处有一固定的正点电荷,B 点为 AC 的中点,C 点位于圆周的最低点。现有一个质量为 m、电荷量为 q 套在杆上的带负电的小球(可视为质点)从 A 点由静止开始沿杆下滑。已知重力加速度为 g,A 点距过 C 点的水平面的竖直高度为 3R,小球滑到 B 点时的速度大小为 $ 2\sqrt{gR} $。求：

(1)小球滑至 C 点时的速度的大小。
(2)A、B 两点间的电势差。
(3)若以 C 点作为参考点(零电势点),试确定 A 点的电势。

答案：
(1)解：A到B过程，由动能定理得：
$ mgh_{AB} + qU_{AB} = \frac{1}{2}mv_{B}^{2} - 0 $
A到C过程，由动能定理得：
$ mgh_{AC} + qU_{AC} = \frac{1}{2}mv_{C}^{2} - 0 $
因B、C在同一等势面上，$U_{AC}=U_{AB}$，$h_{AC}=3R$，$h_{AB}=\frac{3R}{2}$
联立解得：$v_{C}=\sqrt{7gR}$
(2)解：由
(1)中A到B过程方程：
$ mg\cdot \frac{3R}{2} + qU_{AB} = \frac{1}{2}m(2\sqrt{gR})^{2} $
解得：$U_{AB}=-\frac{mgR}{2q}$
(3)解：因B、C等势，$φ_{B}=φ_{C}=0$
$U_{AB}=φ_{A}-φ_{B}=φ_{A}$
故$φ_{A}=-\frac{mgR}{2q}$
答案：
(1)$\sqrt{7gR}$；
(2)$-\frac{mgR}{2q}$；
(3)$-\frac{mgR}{2q}$