《2025年暑假作业甘肃少年儿童出版社高一物理人教版》

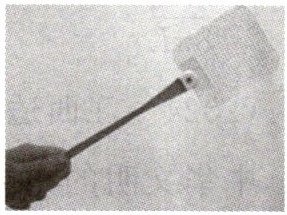
1. 夏天苍蝇格外多,此时我们会用苍蝇拍拍打。生活经验告诉我们：我们用苍蝇拍拍打苍蝇时,苍蝇拍把手长的明显要比把手短的效果好,这是因为使用把手长的拍子打苍蝇时(C)

A.拍子给苍蝇的作用力大
B.由于拍子转动角速度大而易打到苍蝇
C.由于拍子转动线速度大而易打到苍蝇
D.感觉错误,长短均一样

答案： 要打到苍蝇需提高拍头线速度。使用苍蝇拍时，可认为人转动角速度$\omega$一定，根据公式$v = r\omega$（其中$v$为线速度，$r$为转动半径，$\omega$为角速度），把手长的拍子转动半径$r$更大，拍头线速度$v$更大，故易打到苍蝇。
答案：C

2. 如图是一种叫“指尖陀螺”的玩具。当将陀螺绕位于中心A的转轴旋转时,陀螺上B、C两点的周期、角速度及线速度的关系正确的是(B)

A.$ T_{B}= T_{C},v_{B}＞v_{C} $
B.$ T_{B}= T_{C},v_{B}＜v_{C} $
C.$ \omega_{B}= \omega_{C},v_{B}= v_{C} $
D.$ \omega_{B}＜\omega_{C},v_{B}＜v_{C} $

答案： 解：B、C两点同轴转动，故周期$T_B=T_C$，角速度$\omega_B=\omega_C$。
由图可知，$r_C ＞ r_B$，根据$v=\omega r$，得$v_C ＞ v_B$。
结论：$T_B=T_C$，$v_B ＜ v_C$。
答案：B

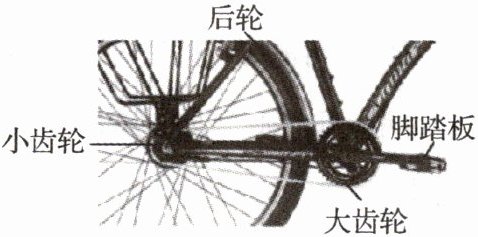
3. 某同学以“自行车的齿轮传动”作为探究学习的课题。该同学通过观察发现,自行车的大齿轮与小齿轮通过链条相连,后轮与小齿轮绕共同的轴转动。脚踏板如图所示,测得大齿轮的半径为$ r_{1} $,小齿轮的半径为$ r_{2} $,自行车后轮的半径为$ R $。若测得在时间$ t 内大齿轮转动的圈数为 N $,则自行车前进的速度大小表达式为(C)

A.$ \frac{2\pi R}{t} $
B.$ \frac{\pi NRr_{2}}{r_{1}t} $
C.$ \frac{2\pi NRr_{1}}{r_{2}t} $
D.$ \frac{2\pi Rtr_{2}}{r_{1}N} $

答案： 解：大齿轮的角速度$\omega_{1}=\frac{2\pi N}{t}$，
大齿轮边缘线速度$v_{1}=\omega_{1}r_{1}=\frac{2\pi N r_{1}}{t}$，
因链条传动，小齿轮边缘线速度$v_{2}=v_{1}=\frac{2\pi N r_{1}}{t}$，
小齿轮角速度$\omega_{2}=\frac{v_{2}}{r_{2}}=\frac{2\pi N r_{1}}{t r_{2}}$，
后轮与小齿轮同轴，角速度相同，后轮边缘线速度即自行车前进速度$v=\omega_{2}R=\frac{2\pi N R r_{1}}{r_{2}t}$。
答案：C

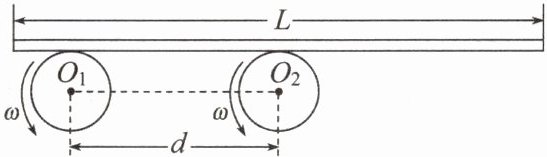
4. 如图所示,两个轮子的半径均为$ R $,两轮的转轴$ O_{1} $、$ O_{2} $在同一水平面上,相互平行,相距为$ d $,两轮均以角速度$ \omega $逆时针方向匀速转动。将一长木板置于两轮上,当木板的重心位于右轮正上方时,木板与两轮间已不再有相对滑动。若木板的长度$ L＞2d $,则木板的重心由右轮正上方移到左轮正上方所需的时间是(B)

A.$ \frac{2\pi}{\omega} $
B.$ \frac{d}{\omega R} $
C.$ \frac{d}{\omega} $
D.$ \frac{R}{\omega} $

答案： 解：木板与两轮间无相对滑动时，木板运动速度 $ v = \omega R $。
木板重心位移大小为 $ d $，由 $ d = vt $ 得 $ d = \omega Rt $。
解得 $ t = \frac{d}{\omega R} $。
答案：B

5. 如图所示为明代出版的《天工开物》一书中的牛力齿轮翻车的画面,若A、B两齿轮半径的大小关系为$ r_{A}= 1.5r_{B} $,下列说法正确的是(BC)

A.齿轮A、B的角速度大小关系为$ \omega_{A}= \omega_{B} $
B.齿轮A、B的角速度大小关系为$ 3\omega_{A}= 2\omega_{B} $
C.齿轮A、B边缘的线速度大小关系为$ v_{A}= v_{B} $
D.齿轮A、B边缘的线速度大小关系为$ 2v_{A}= 3v_{B} $

答案： 齿轮A与齿轮B是同缘传动，边缘点线速度大小相等，即$v_{A}=v_{B}$，C正确，D错误；
已知$r_{A}=1.5r_{B}$，由$v = \omega r$可得$\omega_{A}r_{A}=\omega_{B}r_{B}$，即$\omega_{A}×1.5r_{B}=\omega_{B}r_{B}$，化简得$3\omega_{A}=2\omega_{B}$，B正确，A错误。
答案：B、C

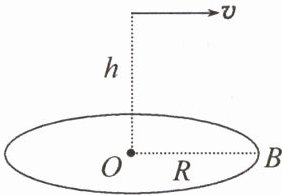
6. 如图所示,半径为$ R $的圆盘绕垂直于盘面的中心轴匀速转动,其正上方$ h 处沿 OB $方向水平抛出一小球,要使球与盘只碰一次,且落点为B,求小球的初速度大小及圆盘转动的角速度$ \omega $的大小。

答案： 解：小球做平抛运动，竖直方向：$h = \frac{1}{2}gt^2$，解得运动时间$t = \sqrt{\frac{2h}{g}}$。
水平方向：$R = v_0t$，则小球初速度$v_0 = \frac{R}{t} = R\sqrt{\frac{g}{2h}}$。
圆盘转动，要使球与盘只碰一次且落点为B，圆盘转动周期$T = \frac{2\pi}{\omega}$，运动时间$t = nT$（$n = 1,2,3\cdots$），即$\sqrt{\frac{2h}{g}} = n \cdot \frac{2\pi}{\omega}$，解得$\omega = 2\pi n\sqrt{\frac{g}{2h}}$（$n = 1,2,3\cdots$）。
小球初速度大小为$R\sqrt{\frac{g}{2h}}$，圆盘转动的角速度大小为$2\pi n\sqrt{\frac{g}{2h}}$（$n = 1,2,3\cdots$）。