《2025年暑假作业甘肃少年儿童出版社高一物理人教版》

1. 地球半径为 $ R $,地球表面的重力加速度为 $ g $,若高空中某处的重力加速度为 $ \frac{1}{2}g $,则该处距地球表面的高度为(A)
A.$ (\sqrt{2}-1)R $
B.$ R $
C.$ \sqrt{2}R $
D.$ 2R $

答案： 解：设地球质量为$M$，物体质量为$m$，地球表面处重力加速度为$g$，由万有引力近似等于重力得：$G\frac{Mm}{R^{2}} = mg$。
设高空中某处距地球表面高度为$h$，此处重力加速度为$\frac{1}{2}g$，则有：$G\frac{Mm}{(R + h)^{2}}=m\cdot\frac{1}{2}g$。
联立两式：$\frac{G\frac{Mm}{(R + h)^{2}}}{G\frac{Mm}{R^{2}}}=\frac{m\cdot\frac{1}{2}g}{mg}$，化简得$\frac{R^{2}}{(R + h)^{2}}=\frac{1}{2}$。
解得$(R + h)^{2}=2R^{2}$，$R + h=\sqrt{2}R$，$h = (\sqrt{2}-1)R$。
答案：A

2. 下列说法正确的是(D)
A.海王星是人们直接应用万有引力定律计算出轨道而发现的
B.天王星是人们依据万有引力定律计算出轨道而发现的
C.海王星是人们经过长期的太空观测而发现的
D.天王星的运行轨道与由万有引力定律计算的轨道存在偏差,其原因是天王星受到轨道外的行星的引力作用,由此人们发现了海王星

答案： 解：A.海王星是根据万有引力定律计算出轨道后发现的，但不是直接计算轨道发现，而是通过天王星轨道偏差推测后观测发现，A错误。
B.天王星是通过长期观测发现的，并非依据万有引力定律计算轨道发现，B错误。
C.海王星不是长期太空观测直接发现，而是先计算预测后观测证实，C错误。
D.天王星运行轨道与万有引力定律计算轨道存在偏差，原因是受轨道外行星引力作用，由此发现海王星，D正确。
结论：D

3. 量纲分析是物理学中的一种很重要的研究方法。人类通过实验测量了几个铅球之间的引力,并推算出引力常量 $ G $ 的值。根据推断,下列关于 $ G $ 的具体单位,表述正确的是(B)
A.$ \text{N}\cdot\text{m}/\text{kg} $
B.$ \text{N}\cdot\text{m}^2/\text{kg}^2 $
C.$ \text{N}\cdot\text{kg}^2/\text{m}^2 $
D.$ \text{N}\cdot\text{m}^2\cdot\text{kg}^2 $

答案： 解：由万有引力公式$F = \frac{Gm_1m_2}{r^2}$可得$G=\frac{Fr^2}{m_1m_2}$。
$F$的单位为$N$，$r$的单位为$m$，$m_1$、$m_2$的单位为$kg$，则$G$的单位为$\frac{N \cdot m^2}{kg^2}$，即$N\cdot m^2/kg^2$。
故选 B。

4. (2023·山东等级考)牛顿认为物体落地是由于地球对物体的吸引,这种吸引力可能与天体间(如地球与月球)的引力具有相同的性质,且都满足 $ F\propto\frac{Mm}{r^2} $。已知地月之间的距离 $ r $ 大约是地球半径的 60 倍,地球表面的重力加速度为 $ g $,根据牛顿的猜想,月球绕地球公转的周期为(C)
A.$ 30\pi\sqrt{\frac{r}{g}} $
B.$ 30\pi\sqrt{\frac{g}{r}} $
C.$ 120\pi\sqrt{\frac{r}{g}} $
D.$ 120\pi\sqrt{\frac{g}{r}} $

答案： C 设地球半径为$R$，在地球表面，忽略地球自转，万有引力等于重力：$G\frac{m_{地}m}{R^2}=mg$，月球绕地球做匀速圆周运动，万有引力充当向心力：$G\frac{m_{地}m_{月}}{r^2}=m_{月}\frac{4\pi^2}{T^2}r$，由题意得：$r = 60R$
联立解得：$T = 120\pi\sqrt{\frac{r}{g}}$，故 A、B、D 错误，C 正确。

5. 2008年,我国天文学家利用国家天文台兴隆观测基地的2.16米望远镜,发现了一颗绕恒星HD173416运动的系外行星HD173416b,2019年,该恒星和行星被国际天文学联合会分别命名为“羲和”和“望舒”,天文观测得到恒星羲和的质量是太阳质量的2倍,若将望舒与地球的公转均视为匀速圆周运动,且公转的轨道半径相等。则望舒与地球公转速度大小的比值为(C)
A.$ 2\sqrt{2} $
B.2
C.$ \sqrt{2} $
D.$ \frac{\sqrt{2}}{2} $

答案： 解：地球绕太阳公转和行星望舒绕恒星羲和的匀速圆周运动，万有引力提供向心力，有$G\frac{Mm}{r^2}=m\frac{v^2}{r}$，解得$v=\sqrt{\frac{GM}{r}}$。
恒星羲和质量$M_羲=2M_太$，轨道半径$r_望=r_地$。
望舒公转速度$v_望=\sqrt{\frac{GM_羲}{r_望}}=\sqrt{\frac{G\cdot2M_太}{r_地}}$，地球公转速度$v_地=\sqrt{\frac{GM_太}{r_地}}$。
则$\frac{v_望}{v_地}=\frac{\sqrt{\frac{2GM_太}{r_地}}}{\sqrt{\frac{GM_太}{r_地}}}=\sqrt{2}$。
答案：C

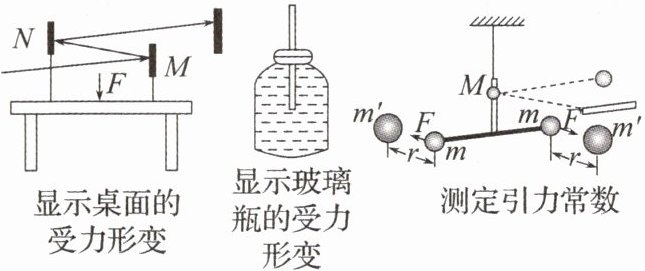
6. 如图所示是力学中的三个实验装置。这三个实验共同的物理方法是(C)

A.极限的方法
B.控制变量的方法
C.放大的方法
D.等效的方法

答案： C。解析：桌面受力形变时，微小形变借助光的反射放大；玻璃瓶受力形变时，通过细管中液面高度变化放大液体体积变化；测定引力常数时，借助光的反射放大转动角度。三个实验均采用放大的方法。

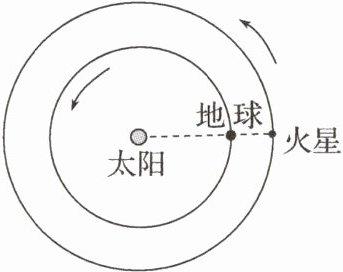
7. (2023·湖北选择考)2022年12月8日,地球恰好运行到火星和太阳之间,且三者几乎排成一条直线,此现象被称为“火星冲日”。火星和地球几乎在同一平面内沿同一方向绕太阳做圆周运动,火星与地球的公转轨道半径之比约为 $ 3:2 $,如图所示。根据以上信息可以得出(B)

A.火星与地球绕太阳运动的周期之比约为 $ 27:8 $
B.当火星与地球相距最远时,两者的相对速度最大
C.火星与地球表面的自由落体加速度大小之比约为 $ 9:4 $
D.下一次“火星冲日”将出现在2023年12月8日之前

答案： A. 根据开普勒第三定律：$\frac{r_{火}^{3}}{r_{地}^{3}} = \frac{T_{火}^{2}}{T_{地}^{2}}$，$\frac{r_{火}}{r_{地}}=\frac{3}{2}$，则$\frac{T_{火}}{T_{地}}=\sqrt{(\frac{3}{2})^{3}}=\frac{3\sqrt{6}}{4}\neq\frac{27}{8}$，A错误。
B. 火星与地球均绕太阳做匀速圆周运动，速度大小不变。相距最远时速度方向相反，相对速度$v_{相对}=v_{地}+v_{火}$；相距最近时速度方向相同，相对速度$v_{相对}=|v_{地}-v_{火}|$，故相距最远时相对速度最大，B正确。
C. 星球表面自由落体加速度$g=\frac{GM}{R^{2}}$，因未知火星与地球的质量$M$及半径$R$，无法得出加速度之比，C错误。
D. 地球角速度$\omega_{地}=\frac{2\pi}{T_{地}}$，火星角速度$\omega_{火}=\frac{2\pi}{T_{火}}$，下次冲日时地球比火星多转$2\pi$，即$(\omega_{地}-\omega_{火})t = 2\pi$，$t=\frac{T_{火}T_{地}}{T_{火}-T_{地}}$。由A知$T_{火}＞T_{地}$，则$t＞T_{地}$（1年），故下次冲日在2023年12月8日之后，D错误。
答案：B