2025年暑假作业甘肃少年儿童出版社高一物理人教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年暑假作业甘肃少年儿童出版社高一物理人教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
7. 如图甲所示是一架战机的起飞过程,该战机质量为 m,以恒定的功率 P 启动,其速度随时间变化的图像如图乙所示,经过时间 $ t _ { 0 } $,战机达到最大速度 $ v _ { \mathrm { m } } $ 时刚好起飞,关于战机起飞过程,下列说法正确的是 (
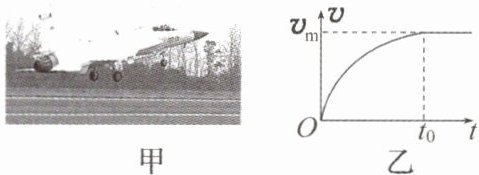
A.发动机的牵引力做功为 $ P t _ { 0 } $
B.战机滑行的位移等于 $ \frac { v _ { \mathrm { m } } t _ { 0 } } { 2 } $
C.发动机的牵引力所做的功大于 $ \frac { 1 } { 2 } m v _ { \mathrm { m } } ^ { 2 } $
D.战机克服阻力所做的功为 $ P t _ { 0 } - \frac { 1 } { 2 } m v _ { \mathrm { m } } ^ { 2 } $
ACD
)
A.发动机的牵引力做功为 $ P t _ { 0 } $
B.战机滑行的位移等于 $ \frac { v _ { \mathrm { m } } t _ { 0 } } { 2 } $
C.发动机的牵引力所做的功大于 $ \frac { 1 } { 2 } m v _ { \mathrm { m } } ^ { 2 } $
D.战机克服阻力所做的功为 $ P t _ { 0 } - \frac { 1 } { 2 } m v _ { \mathrm { m } } ^ { 2 } $
答案:
解:A. 发动机以恒定功率 $ P $ 启动,牵引力做功 $ W = Pt_0 $,A 正确;
B. 由 $ v-t $ 图像知,战机做加速度减小的加速运动,其位移大于匀加速运动的位移 $ \frac{v_m t_0}{2} $,B 错误;
C. 根据动能定理 $ Pt_0 - W_f = \frac{1}{2}mv_m^2 $,则 $ Pt_0 = \frac{1}{2}mv_m^2 + W_f $,故牵引力做功 $ Pt_0 > \frac{1}{2}mv_m^2 $,C 正确;
D. 由动能定理得,克服阻力做功 $ W_f = Pt_0 - \frac{1}{2}mv_m^2 $,D 正确。
答案:A、C、D
B. 由 $ v-t $ 图像知,战机做加速度减小的加速运动,其位移大于匀加速运动的位移 $ \frac{v_m t_0}{2} $,B 错误;
C. 根据动能定理 $ Pt_0 - W_f = \frac{1}{2}mv_m^2 $,则 $ Pt_0 = \frac{1}{2}mv_m^2 + W_f $,故牵引力做功 $ Pt_0 > \frac{1}{2}mv_m^2 $,C 正确;
D. 由动能定理得,克服阻力做功 $ W_f = Pt_0 - \frac{1}{2}mv_m^2 $,D 正确。
答案:A、C、D
8. 一物块以初速度 $ v _ { 0 } $ 自固定斜面底端沿斜面向上运动,一段时间后回到斜面底端。该物块的动能 $ E _ { \mathrm { k } } $ 随位移 x 的变化关系如图所示,图中 $ x _ { 0 } $、$ E _ { \mathrm { k } 1 } $、$ E _ { \mathrm { k } 2 } $ 均已知。根据图中信息可以求出的物理量有 (
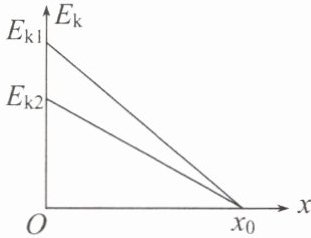
A.重力加速度大小
B.物块所受滑动摩擦力的大小
C.斜面的倾角
D.沿斜面上滑的时间
BD
)
A.重力加速度大小
B.物块所受滑动摩擦力的大小
C.斜面的倾角
D.沿斜面上滑的时间
答案:
解:
1. 由图像知,初动能 $ E_{k1} = \frac{1}{2}mv_0^2 $,可解得物块质量 $ m $。
2. 上滑过程:根据动能定理 $ E_k - E_{k1} = -(mg\sin\theta + f)x $,图像斜率绝对值为合外力,即 $ mg\sin\theta + f = \frac{E_{k1}}{x_0} $。
3. 下滑过程:根据动能定理 $ E_k = (mg\sin\theta - f)(x_0 - x) $,图像斜率为合外力,即 $ mg\sin\theta - f = \frac{E_{k2}}{x_0} $。
4. 联立上滑、下滑方程解得:
滑动摩擦力 $ f = \frac{E_{k1} - E_{k2}}{2x_0} $(可求);
$ g\sin\theta = \frac{E_{k1} + E_{k2}}{2mx_0} $(因 $ g $、$\theta$ 均未知,无法单独求出)。
5. 上滑时间:由牛顿第二定律 $ mg\sin\theta + f = ma $,结合 $ v_0^2 = 2ax_0 $ 或 $ t = \frac{v_0}{a} $,解得 $ t = \frac{2x_0}{v_0} = \frac{2x_0}{\sqrt{\frac{2E_{k1}}{m}}} = x_0\sqrt{\frac{2m}{E_{k1}}} $(可求)。
结论:可求出的物理量为 B、D。
答案:B、D
1. 由图像知,初动能 $ E_{k1} = \frac{1}{2}mv_0^2 $,可解得物块质量 $ m $。
2. 上滑过程:根据动能定理 $ E_k - E_{k1} = -(mg\sin\theta + f)x $,图像斜率绝对值为合外力,即 $ mg\sin\theta + f = \frac{E_{k1}}{x_0} $。
3. 下滑过程:根据动能定理 $ E_k = (mg\sin\theta - f)(x_0 - x) $,图像斜率为合外力,即 $ mg\sin\theta - f = \frac{E_{k2}}{x_0} $。
4. 联立上滑、下滑方程解得:
滑动摩擦力 $ f = \frac{E_{k1} - E_{k2}}{2x_0} $(可求);
$ g\sin\theta = \frac{E_{k1} + E_{k2}}{2mx_0} $(因 $ g $、$\theta$ 均未知,无法单独求出)。
5. 上滑时间:由牛顿第二定律 $ mg\sin\theta + f = ma $,结合 $ v_0^2 = 2ax_0 $ 或 $ t = \frac{v_0}{a} $,解得 $ t = \frac{2x_0}{v_0} = \frac{2x_0}{\sqrt{\frac{2E_{k1}}{m}}} = x_0\sqrt{\frac{2m}{E_{k1}}} $(可求)。
结论:可求出的物理量为 B、D。
答案:B、D
9. (16 分)如图甲所示为游乐园的过山车,其局部可简化为如图乙所示的示意图,倾角 $ \theta = 37 ^ { \circ } $ 的两轨道 BC、DE 的下端与水平半圆轨道 CD 相连,倾斜轨道 BC 的 B 端高度 $ h = 24 \mathrm { \ m } $,倾斜轨道 DE 与圆弧 EF 相切于 E 点,圆弧 EF 的圆心 $ O _ { 1 } $、水平半圆轨道 CD 的圆心 $ O _ { 2 } $ 与 A 点在同一水平面上,$ D O _ { 1 } $ 的距离 $ L = 20 \mathrm { \ m } $。质量 $ m = 1 0 0 0 \mathrm { \ kg } $ 的过山车(包含乘客)从 B 点由静止滑下,经过水平半圆轨道后,滑上另一倾斜轨道,到达弧顶时的速度为 $ 3 \sqrt { 1 0 } \mathrm { \ m / s } $,已知过山车在 BCDE 段运动时所受的摩擦力与轨道对过山车的支持力成正比,比例系数为 $ \mu = \frac { 1 } { 3 2 } $,EF 段摩擦力不计,整个过程空气阻力不计。求

(1)从 B 到 F 摩擦力对小车做的功。
(2)如果过 D 点时,发现轨道 EF 有故障,为保障乘客安全,立即采取制动措施,使小车不能到达 EF 段,则小车受到的摩擦力至少多大?

(1)从 B 到 F 摩擦力对小车做的功。
(2)如果过 D 点时,发现轨道 EF 有故障,为保障乘客安全,立即采取制动措施,使小车不能到达 EF 段,则小车受到的摩擦力至少多大?
答案:
(1) 设水平半圆轨道半径为 $ R $,由几何关系知 $ h = R(1 + \sin\theta) $,$\sin37^\circ = 0.6$,解得 $ R = 15 \, \text{m} $。$ O_1 $ 与 $ A $ 等高,$ DO_1 = L = 20 \, \text{m} $,$ DE $ 轨道长度 $ x_{DE} = \frac{L}{\cos\theta} = 25 \, \text{m} $,$ DE $ 高度 $ h_{DE} = x_{DE}\sin\theta = 15 \, \text{m} $,$ F $ 点高度 $ h_F = R + h_{DE} = 30 \, \text{m} $。
对 $ B $ 到 $ F $ 由动能定理:$ mg(h - h_F) + W_f = \frac{1}{2}mv_F^2 - 0 $,代入 $ m = 1000 \, \text{kg} $,$ v_F = 3\sqrt{10} \, \text{m/s} $,解得 $ W_f = -7.5 × 10^4 \, \text{J} $。
(2) 小车不能到达 $ EF $ 段,即最高到达 $ E $ 点速度为 0。$ B $ 到 $ E $ 过程,$ BC $ 长度 $ x_{BC} = \frac{h - R}{\sin\theta} = 15 \, \text{m} $,摩擦力做功 $ W_{f1} = -\mu mg\cos\theta(x_{BC} + x_{DE}) - \mu mg \cdot \pi R = -6 × 10^4 \, \text{J} $。
由动能定理:$ mg(h - h_{DE}) + W_{f1} - f x_{DE} = 0 - 0 $,解得 $ f = 4.6 × 10^3 \, \text{N} $。
(1) $-7.5 × 10^4 \, \text{J}$
(2) $4.6 × 10^3 \, \text{N}$
(1) 设水平半圆轨道半径为 $ R $,由几何关系知 $ h = R(1 + \sin\theta) $,$\sin37^\circ = 0.6$,解得 $ R = 15 \, \text{m} $。$ O_1 $ 与 $ A $ 等高,$ DO_1 = L = 20 \, \text{m} $,$ DE $ 轨道长度 $ x_{DE} = \frac{L}{\cos\theta} = 25 \, \text{m} $,$ DE $ 高度 $ h_{DE} = x_{DE}\sin\theta = 15 \, \text{m} $,$ F $ 点高度 $ h_F = R + h_{DE} = 30 \, \text{m} $。
对 $ B $ 到 $ F $ 由动能定理:$ mg(h - h_F) + W_f = \frac{1}{2}mv_F^2 - 0 $,代入 $ m = 1000 \, \text{kg} $,$ v_F = 3\sqrt{10} \, \text{m/s} $,解得 $ W_f = -7.5 × 10^4 \, \text{J} $。
(2) 小车不能到达 $ EF $ 段,即最高到达 $ E $ 点速度为 0。$ B $ 到 $ E $ 过程,$ BC $ 长度 $ x_{BC} = \frac{h - R}{\sin\theta} = 15 \, \text{m} $,摩擦力做功 $ W_{f1} = -\mu mg\cos\theta(x_{BC} + x_{DE}) - \mu mg \cdot \pi R = -6 × 10^4 \, \text{J} $。
由动能定理:$ mg(h - h_{DE}) + W_{f1} - f x_{DE} = 0 - 0 $,解得 $ f = 4.6 × 10^3 \, \text{N} $。
(1) $-7.5 × 10^4 \, \text{J}$
(2) $4.6 × 10^3 \, \text{N}$
查看更多完整答案,请扫码查看


