第46页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
3. 如图,已知 $ AB // CD $,那么 $ \angle A + \angle C + \angle AEC = $(
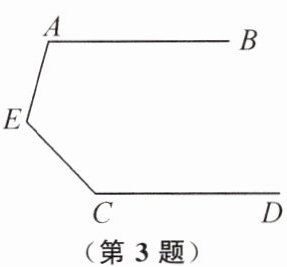
A.$ 360^\circ $
B.$ 270^\circ $
C.$ 200^\circ $
D.$ 180^\circ $
A
)
A.$ 360^\circ $
B.$ 270^\circ $
C.$ 200^\circ $
D.$ 180^\circ $
答案:
A
4. 如图,$ CD // BE $,则 $ \angle 2 + \angle 3 - \angle 1 $ 的度数等于(
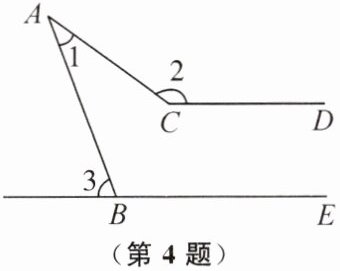
A.$ 90^\circ $
B.$ 120^\circ $
C.$ 150^\circ $
D.$ 180^\circ $
D
)
A.$ 90^\circ $
B.$ 120^\circ $
C.$ 150^\circ $
D.$ 180^\circ $
答案:
D
5. 如图,已知 $ AB // DE $,$ \angle ABC = 80^\circ $,$ \angle CDE = 140^\circ $,则 $ \angle BCD = $

$40^{\circ}$
。
答案:
$40^{\circ}$
6. 如图,已知 $ AE // BD $,$ \angle 1 = 130^\circ $,$ \angle 2 = 30^\circ $,则 $ \angle C = $
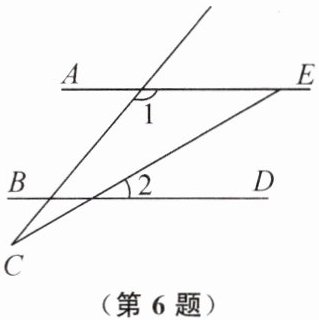
$20^{\circ}$
。
答案:
$20^{\circ}$
7. 如图,已知 $ AB // CD $,$ \angle ABE = 120^\circ $,$ \angle DCE = 35^\circ $,则 $ \angle BEC = $

$95^{\circ}$
。
答案:
$95^{\circ}$
8. 如图,$ l // m $,长方形 $ ABCD $ 的顶点 $ B $ 在直线 $ m $ 上,则 $ \angle \alpha = $
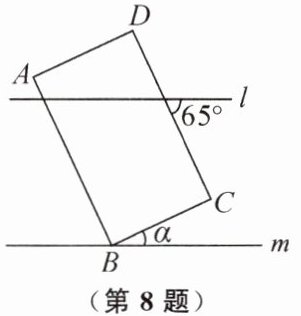
$25^{\circ}$
。
答案:
$25^{\circ}$
9. 如图,直线 $ l_1 // l_2 $,$ \angle \alpha = \angle \beta $,$ \angle 1 = 40^\circ $,则 $ \angle 2 = $
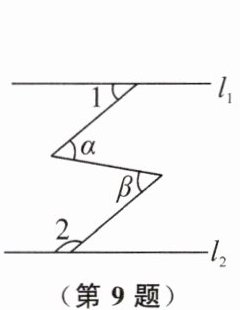
140
$ ^\circ $。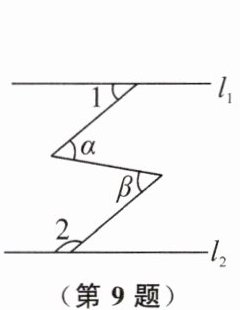
答案:
$140^{\circ}$
10. 已知 $ EM // BN $。
(1)如图①,求 $ \angle E + \angle A + \angle B $ 的度数,并说明理由。
(2)如图②,$ \angle AEM $ 与 $ \angle ABN $ 的平分线相交于点 $ F $,分别交 $ BN $,$ EM $ 于 $ C $,$ D $ 两点。
① 若 $ \angle A = 120^\circ $,$ \angle AEM = 140^\circ $,则 $ \angle EFD = $______
② 试探究 $ \angle EFD $ 与 $ \angle A $ 的数量关系,并说明理由。
(3)如图③,$ \angle AEM $ 与 $ \angle ABN $ 的平分线相交于点 $ F $,过点 $ F $ 作 $ FG \perp BD $ 交 $ BN $ 于点 $ G $。若 $ 4 \angle A = 3 \angle EFG $,求 $ \angle EFB $ 的度数。
(1)如图①,求 $ \angle E + \angle A + \angle B $ 的度数,并说明理由。
(2)如图②,$ \angle AEM $ 与 $ \angle ABN $ 的平分线相交于点 $ F $,分别交 $ BN $,$ EM $ 于 $ C $,$ D $ 两点。
① 若 $ \angle A = 120^\circ $,$ \angle AEM = 140^\circ $,则 $ \angle EFD = $______
60°
;② 试探究 $ \angle EFD $ 与 $ \angle A $ 的数量关系,并说明理由。
(3)如图③,$ \angle AEM $ 与 $ \angle ABN $ 的平分线相交于点 $ F $,过点 $ F $ 作 $ FG \perp BD $ 交 $ BN $ 于点 $ G $。若 $ 4 \angle A = 3 \angle EFG $,求 $ \angle EFB $ 的度数。
54°
答案:
(1) $\angle E+\angle A+\angle B=360^{\circ}$,理由略。
(2) ① $60^{\circ}$
② $\angle A=2\angle EFD$。理由如下:由
(1)知 $\angle AEM+\angle A+\angle ABN=360^{\circ}$,$\therefore \angle ABN=360^{\circ}-\angle AEM-\angle A$。$\because \angle AEM$ 与 $\angle ABN$ 的平分线相交于点 $F$,$\therefore \angle DEF=\frac{1}{2}\angle AEM$,$\angle FBC=\frac{1}{2}\angle ABN$。$\because EM// BN$,$\therefore \angle EDF=\angle FBC=\frac{1}{2}\angle ABN$,$\therefore \angle EFD=180^{\circ}-\angle DEF-\angle EDF=180^{\circ}-\frac{1}{2}\angle AEM-\frac{1}{2}\angle ABN=180^{\circ}-\frac{1}{2}(360^{\circ}-\angle A)=\frac{1}{2}\angle A$,即 $\angle A=2\angle EFD$。
(3) 设 $\angle EFD=x$,则易证 $\angle A=2x$。由题意,得 $4× 2x=3(90^{\circ}+x)$,解得 $x=54^{\circ}$,即 $\angle EFB=54^{\circ}$。
(1) $\angle E+\angle A+\angle B=360^{\circ}$,理由略。
(2) ① $60^{\circ}$
② $\angle A=2\angle EFD$。理由如下:由
(1)知 $\angle AEM+\angle A+\angle ABN=360^{\circ}$,$\therefore \angle ABN=360^{\circ}-\angle AEM-\angle A$。$\because \angle AEM$ 与 $\angle ABN$ 的平分线相交于点 $F$,$\therefore \angle DEF=\frac{1}{2}\angle AEM$,$\angle FBC=\frac{1}{2}\angle ABN$。$\because EM// BN$,$\therefore \angle EDF=\angle FBC=\frac{1}{2}\angle ABN$,$\therefore \angle EFD=180^{\circ}-\angle DEF-\angle EDF=180^{\circ}-\frac{1}{2}\angle AEM-\frac{1}{2}\angle ABN=180^{\circ}-\frac{1}{2}(360^{\circ}-\angle A)=\frac{1}{2}\angle A$,即 $\angle A=2\angle EFD$。
(3) 设 $\angle EFD=x$,则易证 $\angle A=2x$。由题意,得 $4× 2x=3(90^{\circ}+x)$,解得 $x=54^{\circ}$,即 $\angle EFB=54^{\circ}$。
查看更多完整答案,请扫码查看


