《2025年拔尖特训四年级数学上册苏教版江苏专版》

1. 看量角器上的刻度,填出每个角各是多少度。

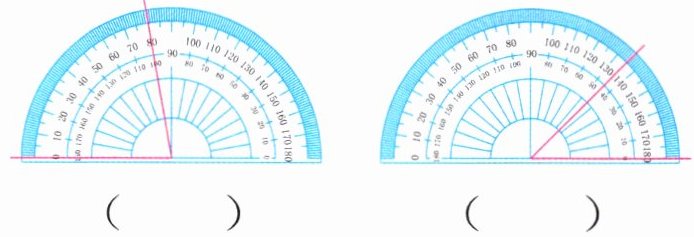
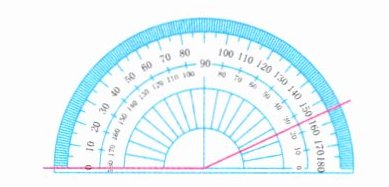
(80°) (45°)

(155°)

答案： 80° 45° 155°

2. (几何直观)下面的图形各由几条线段围成？各有几个角？

5588

答案： 5 5 8 8

(1)(扬州江都区)学校举行放风筝比赛,规定用一样长的风筝线。将风筝线的一端固定在地面上,下面是三只风筝的风筝线与地面形成的角的度数,飞得最高的是(A)。
A.$75^{\circ}$
B.$30^{\circ}$
C.$120^{\circ}$

答案：
(1) A

(2)测量一个角,角的一条边对应量角器上的$180^{\circ}$刻度线,另一条边对应同一圈的$20^{\circ}$刻度线。这个角的度数是(C)。
A.$70^{\circ}$
B.$180^{\circ}$
C.$160^{\circ}$

答案：
(2) C 解析:因为角的一条边对应量角器上的180°刻度线,另一条边对应同一圈的20°刻度线,所以这个角的度数是180°-20°=160°。

4. (操作探究)用量角器量出下面每个角的度数,并观察所填的度数,你发现了什么？

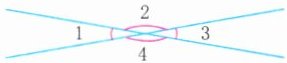
$∠1= $20° $∠2= $160°
$∠3= $20° $∠4= $160°
我发现：相对的两个角的度数相等,相邻的两个角的度数之和是180°。

答案： 20° 160° 20° 160° 相对的两个角的度数相等,相邻的两个角的度数之和是180°

5. 如图,角的顶点与量角器的中心重合,角的另一条边在$0^{\circ}$刻度线上,被遮住的角是多少度？

答案： 可能是60°,也可能是120° 解析:根据量角器的测量方法可知,如果题图中的角的另一条边与内圈的0°刻度线重合,那么被遮住的角是60°;如果题图中的角的另一条边与外圈的0°刻度线重合,那么被遮住的角是120°。

6. *下图中共有多少个角？

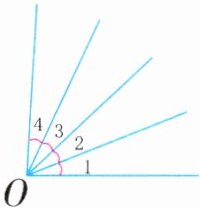
答案： 10个 解析:基础角有4个,由2个基础角组成的角有3个,由3个基础角组成的角有2个,由4个基础角组成的角有1个,所以共有4+3+2+1=10(个)角。 方法归纳＞＞ 数角的方法 数角时有两种方法。方法一:先数基础角,再数由2个基础角组成的角,接着数由3个基础角组成的角……最后相加;方法二:有n条射线,角的总个数就是1+2+3+…+(n-1)。

|直线的条数|1|2|3|4|……|15|
|交点的个数|0|1|3|6|……|105|
|增加的交点个数|0|1|2|3|……|14|

答案： 105 14 解析:观察表格可以发现,随着直线条数的增加,交点个数也在增加,增加的规律是从1开始,依次加到比直线的条数少1的数,前面所增加的这些交点个数的和就是交点的个数。