第53页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
1. (常州溧阳)在$◯$里填“>”“<”或“=”。
$37×14 - 12$
$98 - 25 - 19$
$300÷(5×4) + 210$
$37×14 - 12$
>
$37×(14 - 12)$$98 - 25 - 19$
<
$98 - 25 + 19$$300÷(5×4) + 210$
<
$300÷5×4 + 210$
答案:
> < <
2. 计算下面各题。
$450 - (400÷25 + 75)$
$(97 - 360÷24)×16$
$450 - (400÷25 + 75)$
$(97 - 360÷24)×16$
答案:
359 1312
3. (算理理解)把下面的每组算式写成综合算式。
(1)$900÷20 = 45$ $45 + 19 = 64$ $64×12 = 768$
综合算式:( )
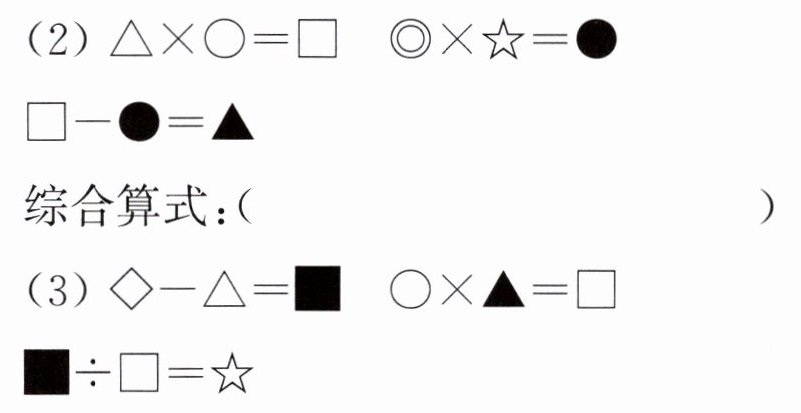
综合算式:( )
(1)$900÷20 = 45$ $45 + 19 = 64$ $64×12 = 768$
综合算式:( )

综合算式:( )
答案:
(1)(900÷20+19)×12=768
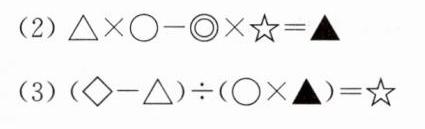
(1)(900÷20+19)×12=768
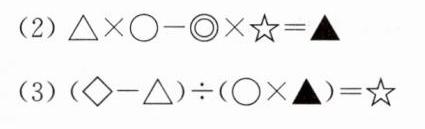
4. (宿迁泗阳)根据运算顺序,给算式添上括号。
$290 + 168÷3×5$ 除→加→乘
$290 + 168÷3×5$ 除→加→乘
答案:
(290+168÷3)×5
5. (南通崇川区)某品牌一款电动汽车原来充足电可以行驶150千米,技术改进后,充足电行驶的路程比原来的2倍还多80千米。技术改进后,该款电动汽车充足电比原来多行驶多少千米?
答案:
150×2+80 - 150 = 230(千米)
6. 若给算式$100÷2×10 + 5$添上一个括号,则使结果最大的算式是什么? 使结果最小的算式是什么? 分别算一算。
答案:
最大:100÷2×(10+5) = 750
最小:100÷(2×10+5) = 4
最小:100÷(2×10+5) = 4
7. $^{\ast}$(模型意识)公路一侧等距离地栽种了一些松树,小乐从第1棵走到第5棵用了16秒。照这样的速度计算,他从第5棵走到第20棵,需要多少秒?
答案:
16÷(5 - 1)×(20 - 5) = 60(秒)
解析:本题属于间隔问题,要先求出走一个间隔用的时间,再求出一共要走多少个间隔。从第1棵走到第5棵用了16秒,走了5 - 1 = 4(个)间隔,求出走一个间隔用了16÷4 = 4(秒)。从第5棵走到第20棵,走了(20 - 5)个间隔,用走一个间隔用的时间乘要走的间隔个数即可得到需要的时间。
方法归纳>>
用综合法解决间隔问题
当两端都栽时,间隔个数 = 棵数 - 1;当一端栽一端不栽时,间隔个数 = 棵数;当两端都不栽时,间隔个数 = 棵数 + 1。本题属于两端都栽的情况,所以间隔个数 = 棵数 - 1。
解析:本题属于间隔问题,要先求出走一个间隔用的时间,再求出一共要走多少个间隔。从第1棵走到第5棵用了16秒,走了5 - 1 = 4(个)间隔,求出走一个间隔用了16÷4 = 4(秒)。从第5棵走到第20棵,走了(20 - 5)个间隔,用走一个间隔用的时间乘要走的间隔个数即可得到需要的时间。
方法归纳>>
用综合法解决间隔问题
当两端都栽时,间隔个数 = 棵数 - 1;当一端栽一端不栽时,间隔个数 = 棵数;当两端都不栽时,间隔个数 = 棵数 + 1。本题属于两端都栽的情况,所以间隔个数 = 棵数 - 1。
查看更多完整答案,请扫码查看


