22. (10分)已知抛物线$y= ax^2+bx+1(a≠0)经过点(1,-2)$,$(-2,19)$。
(1)求$a,b$的值。
(2)若$A(m,p)和B(n,p)$是抛物线上不同的两点,且$m-n= \frac{1}{2}$,求$m,n$的值。
(1)求$a,b$的值。
(2)若$A(m,p)和B(n,p)$是抛物线上不同的两点,且$m-n= \frac{1}{2}$,求$m,n$的值。
答案:
解:
(1)把点$(1,-2)$,$(-2,19)$的坐标代入$y = ax^{2}+bx + 1$得,$\begin{cases}-2 = a + b + 1\\19 = 4a - 2b + 1\end{cases}$,解得$\begin{cases}a = 2\\b = - 5\end{cases}$。
(2)由
(1)得函数表达式为$y = 2x^{2}-5x + 1$,
∴对称轴是直线$x = -\frac{-5}{2×2}=\frac{5}{4}$。$\because A(m,p)$,$B(n,p)$是抛物线上不同的两点,纵坐标相同,
∴$A(m,p)$,$B(n,p)$关于直线$x = \frac{5}{4}$对称,$\therefore \frac{m + n}{2}=\frac{5}{4}$,$\therefore m + n=\frac{5}{2}$。又$\because m - n=\frac{1}{2}$,$\therefore m=\frac{3}{2}$,$n = 1$。
(1)把点$(1,-2)$,$(-2,19)$的坐标代入$y = ax^{2}+bx + 1$得,$\begin{cases}-2 = a + b + 1\\19 = 4a - 2b + 1\end{cases}$,解得$\begin{cases}a = 2\\b = - 5\end{cases}$。
(2)由
(1)得函数表达式为$y = 2x^{2}-5x + 1$,
∴对称轴是直线$x = -\frac{-5}{2×2}=\frac{5}{4}$。$\because A(m,p)$,$B(n,p)$是抛物线上不同的两点,纵坐标相同,
∴$A(m,p)$,$B(n,p)$关于直线$x = \frac{5}{4}$对称,$\therefore \frac{m + n}{2}=\frac{5}{4}$,$\therefore m + n=\frac{5}{2}$。又$\because m - n=\frac{1}{2}$,$\therefore m=\frac{3}{2}$,$n = 1$。
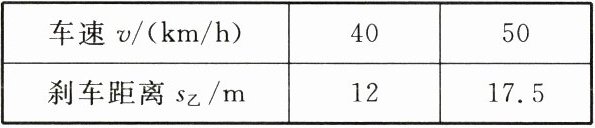
23. (10分)为了解甲、乙两种车的刹车距离,经试验发现,甲车的刹车距离$s_甲(m)是车速v(km/h)的\frac{1}{5}$,乙车的刹车距离$s_乙(m)$等于反应距离与制动距离之和,反应距离与车速$v(km/h)$成正比,制动距离与车速$v^2$成正比,具体关系如下表:
| 车速$v/(km/h)$ | 40 | 50 |
| 刹车距离$s_乙/m$ | 12 | 17.5 |
(1)分别求出$s_甲,s_乙与车速v$的函数关系式。
(2)若乙车在限速$120km/h$的高速公路上行驶,乙车的最大刹车距离是多少?
(3)刹车速度是处理交通事故的一个重要因素,请看下面一个交通事故案例:甲、乙两车在限速为$80km/h$的道路上相向而行,等望见对方,同时刹车时已晚,两车还是相撞了,事后经现场勘查,测得甲车的刹车距离超过$16m$,但小于$18m$,乙车的刹车距离是$24m$,请你比较两车的速度,并判断哪辆车超速?
| 车速$v/(km/h)$ | 40 | 50 |
| 刹车距离$s_乙/m$ | 12 | 17.5 |

(1)分别求出$s_甲,s_乙与车速v$的函数关系式。
(2)若乙车在限速$120km/h$的高速公路上行驶,乙车的最大刹车距离是多少?
(3)刹车速度是处理交通事故的一个重要因素,请看下面一个交通事故案例:甲、乙两车在限速为$80km/h$的道路上相向而行,等望见对方,同时刹车时已晚,两车还是相撞了,事后经现场勘查,测得甲车的刹车距离超过$16m$,但小于$18m$,乙车的刹车距离是$24m$,请你比较两车的速度,并判断哪辆车超速?
答案:
解:
(1)依题意得$s_{甲}=\frac{1}{5}v$。$\because$乙车的反应距离与车速$v$成正比,制动距离与车速$v^{2}$成正比,$\therefore$设$s_{乙}=k_{1}v + k_{2}v^{2}$。由题意得$\begin{cases}12 = 40k_{1}+1600k_{2}\\17.5 = 50k_{1}+2500k_{2}\end{cases}$,解得$\begin{cases}k_{1}=\frac{1}{10}\\k_{2}=\frac{1}{200}\end{cases}$,$\therefore s_{乙}=\frac{1}{200}v^{2}+\frac{1}{10}v$。
(2)$\because$对称轴为直线$v = -\frac{\frac{1}{10}}{2×\frac{1}{200}}=-10$,$\therefore$当$0 < v≤120$时,$s_{乙}$随$v$的增大而增大,即当$v = 120$时,$(s_{乙})_{最大值}=\frac{1}{200}×14400+\frac{1}{10}×120 = 84(m)$,
∴乙车的最大刹车距离为84m。(只要合理解释“当$v = 120$时,$s_{乙}$最大”均可)
(3)$\because$甲车的刹车距离超过16m,但小于18m,$\therefore 16 < \frac{1}{5}v < 18$,即$80 < v < 90$。$\because$乙车的刹车距离是24m,$\therefore \frac{1}{200}v^{2}+\frac{1}{10}v = 24$,解得$v_{1}=60$,$v_{2}=-80$(舍去)。$\because$限速80km/h,$\therefore$甲车超速。
(1)依题意得$s_{甲}=\frac{1}{5}v$。$\because$乙车的反应距离与车速$v$成正比,制动距离与车速$v^{2}$成正比,$\therefore$设$s_{乙}=k_{1}v + k_{2}v^{2}$。由题意得$\begin{cases}12 = 40k_{1}+1600k_{2}\\17.5 = 50k_{1}+2500k_{2}\end{cases}$,解得$\begin{cases}k_{1}=\frac{1}{10}\\k_{2}=\frac{1}{200}\end{cases}$,$\therefore s_{乙}=\frac{1}{200}v^{2}+\frac{1}{10}v$。
(2)$\because$对称轴为直线$v = -\frac{\frac{1}{10}}{2×\frac{1}{200}}=-10$,$\therefore$当$0 < v≤120$时,$s_{乙}$随$v$的增大而增大,即当$v = 120$时,$(s_{乙})_{最大值}=\frac{1}{200}×14400+\frac{1}{10}×120 = 84(m)$,
∴乙车的最大刹车距离为84m。(只要合理解释“当$v = 120$时,$s_{乙}$最大”均可)
(3)$\because$甲车的刹车距离超过16m,但小于18m,$\therefore 16 < \frac{1}{5}v < 18$,即$80 < v < 90$。$\because$乙车的刹车距离是24m,$\therefore \frac{1}{200}v^{2}+\frac{1}{10}v = 24$,解得$v_{1}=60$,$v_{2}=-80$(舍去)。$\because$限速80km/h,$\therefore$甲车超速。
24. (12分)已知二次函数$y= ax^2+bx+3(a≠0)的图象过点(1,0)$。
(1)若该函数图象的对称轴为直线$x= -1$,求该函数的表达式。
(2)在(1)的条件下,当$n≤x≤n+4$时,函数$y有最小值-5$,求$n$的值。
(3)已知$a>0$,二次函数的图象经过点$(x_1,y_1)$,$(x_2,y_2)$,$x_1+x_2= 4$,且$x_1<x_2$,试比较$y_1与y_2$的大小。
(1)若该函数图象的对称轴为直线$x= -1$,求该函数的表达式。
(2)在(1)的条件下,当$n≤x≤n+4$时,函数$y有最小值-5$,求$n$的值。
(3)已知$a>0$,二次函数的图象经过点$(x_1,y_1)$,$(x_2,y_2)$,$x_1+x_2= 4$,且$x_1<x_2$,试比较$y_1与y_2$的大小。
答案:
解:
(1)由已知得$\begin{cases}0 = a + b + 3\\-\frac{b}{2a}=-1\end{cases}$,$\therefore \begin{cases}a = - 1\\b = - 2\end{cases}$,$\therefore y = - x^{2}-2x + 3$。
(2)$\frac{n + n + 4}{2}=n + 2$。①当$n + 2≤-1$,即$n≤-3$时,$x = n$时,$y_{最小值}=-n^{2}-2n + 3 = - 5$,解得$n = - 4$或$n = 2$(舍去);②当$n > - 3$时,$x = n + 4$时,$y_{最小值}=-(n + 4)^{2}-2(n + 4)+3 = - 5$,解得$n = - 2$或$n = - 8$(舍去)。综上所述,$n = - 4$或$n = - 2$。
(3)易得抛物线的对称轴为直线$x=\frac{a + 3}{2a}$。$\because x_{1}+x_{2}=4$,$x_{1}<x_{2}$,$\therefore 2 - x_{1}=x_{2}-2$,当$x=\frac{a + 3}{2a}=2$,即$a = 1$时,$y_{1}=y_{2}$;当$a > 1$时,$y_{1}<y_{2}$;当$0 < a < 1$时,$y_{1}>y_{2}$。
(1)由已知得$\begin{cases}0 = a + b + 3\\-\frac{b}{2a}=-1\end{cases}$,$\therefore \begin{cases}a = - 1\\b = - 2\end{cases}$,$\therefore y = - x^{2}-2x + 3$。
(2)$\frac{n + n + 4}{2}=n + 2$。①当$n + 2≤-1$,即$n≤-3$时,$x = n$时,$y_{最小值}=-n^{2}-2n + 3 = - 5$,解得$n = - 4$或$n = 2$(舍去);②当$n > - 3$时,$x = n + 4$时,$y_{最小值}=-(n + 4)^{2}-2(n + 4)+3 = - 5$,解得$n = - 2$或$n = - 8$(舍去)。综上所述,$n = - 4$或$n = - 2$。
(3)易得抛物线的对称轴为直线$x=\frac{a + 3}{2a}$。$\because x_{1}+x_{2}=4$,$x_{1}<x_{2}$,$\therefore 2 - x_{1}=x_{2}-2$,当$x=\frac{a + 3}{2a}=2$,即$a = 1$时,$y_{1}=y_{2}$;当$a > 1$时,$y_{1}<y_{2}$;当$0 < a < 1$时,$y_{1}>y_{2}$。
查看更多完整答案,请扫码查看


