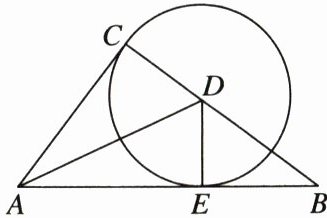
22. (10分)如图,在△ABC中,∠ACB= 90°,AB= 10,AC= 6. 在BC上取一点D,以D为圆心,CD长为半径作⊙D,⊙D恰好与AB相切于点E,连结AD,DE.
(1)求证:AD平分∠BAC.
(2)求⊙D的半径.
(1)求证:AD平分∠BAC.
(2)求⊙D的半径.

答案:
解:
(1)证明:
∵⊙D恰好与AB相切于点E,
∴∠AED=∠DEB=90°.
∵∠ACB=90°,
∴∠ACD=∠AED=90°.
∵DC=DE,AD=AD,
∴Rt△ACD≌Rt△AED(HL),
∴∠CAD=∠EAD,
∴AD平分∠BAC.
(2)设⊙D的半径为r.
在Rt△ACB中,AB=10,AC=6,
∴BC=√(AB² - AC²)=√(10² - 6²)=8.
∵∠ACD=∠BED=90°,∠B=∠B,
∴△BDE∽△BAC,
∴BD/BA=DE/AC,
∴(8 - r)/10=r/6,解得r=3,
∴⊙D的半径为3.
(1)证明:
∵⊙D恰好与AB相切于点E,
∴∠AED=∠DEB=90°.
∵∠ACB=90°,
∴∠ACD=∠AED=90°.
∵DC=DE,AD=AD,
∴Rt△ACD≌Rt△AED(HL),
∴∠CAD=∠EAD,
∴AD平分∠BAC.
(2)设⊙D的半径为r.
在Rt△ACB中,AB=10,AC=6,
∴BC=√(AB² - AC²)=√(10² - 6²)=8.
∵∠ACD=∠BED=90°,∠B=∠B,
∴△BDE∽△BAC,
∴BD/BA=DE/AC,
∴(8 - r)/10=r/6,解得r=3,
∴⊙D的半径为3.
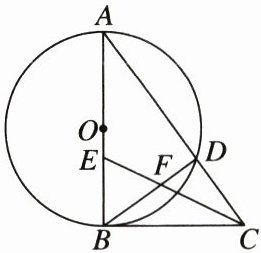
23. (10分)如图,AB为⊙O的直径,点D为⊙O上一点,过点B作⊙O的切线交AD的延长线于点C,CE平分∠ACB,CE,BD交于点F.
(1)求证:BE= BF.
(2)若⊙O的半径为2,$sinA= \frac{3}{5}$,求DF的长度.
(1)求证:BE= BF.
(2)若⊙O的半径为2,$sinA= \frac{3}{5}$,求DF的长度.

答案:
解:
(1)证明:
∵AB为⊙O的直径,
∴∠ADB=90°,∠CDB=90°,
∴∠DCF+∠DFC=90°.
∵BC是⊙O的切线,
∴∠CBE=90°,
∴∠BCE+∠BEC=90°.
∵CE平分∠ACB,
∴∠BCE=∠DCF,
∴∠BEC=∠DFC.
又
∵∠DFC=∠BFE,
∴∠BFE=∠BEF,
∴BE=BF.
(2)如图所示,过点E作EH⊥AC于H.
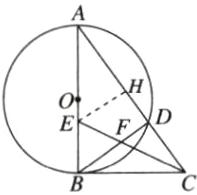
∵CE平分∠ACB,∠ABC=90°,
AC⊥EH,
∴EH=BE=BF.
∵⊙O的半径为2,
∴AB=4.
在Rt△ABC中,sinA=BC/AC=3/5,
设BC=3x,AC=5x,
由勾股定理得AC²=AB²+BC²,
∴4²+(3x)²=(5x)²,
解得x=1(负值舍去),
∴BC=3,AC=5.
∵S△ABC=S△ACE+S△BCE,
∴1/2×4×3=1/2×3BE+1/2×5EH,
∴1/2×4×3=1/2×3BE+1/2×5BE,
∴BE=3/2.
在Rt△ABD中,BD=AB·sinA=12/5,
∴DF=BD - BF=12/5 - 3/2=9/10.
解:
(1)证明:
∵AB为⊙O的直径,
∴∠ADB=90°,∠CDB=90°,
∴∠DCF+∠DFC=90°.
∵BC是⊙O的切线,
∴∠CBE=90°,
∴∠BCE+∠BEC=90°.
∵CE平分∠ACB,
∴∠BCE=∠DCF,
∴∠BEC=∠DFC.
又
∵∠DFC=∠BFE,
∴∠BFE=∠BEF,
∴BE=BF.
(2)如图所示,过点E作EH⊥AC于H.

∵CE平分∠ACB,∠ABC=90°,
AC⊥EH,
∴EH=BE=BF.
∵⊙O的半径为2,
∴AB=4.
在Rt△ABC中,sinA=BC/AC=3/5,
设BC=3x,AC=5x,
由勾股定理得AC²=AB²+BC²,
∴4²+(3x)²=(5x)²,
解得x=1(负值舍去),
∴BC=3,AC=5.
∵S△ABC=S△ACE+S△BCE,
∴1/2×4×3=1/2×3BE+1/2×5EH,
∴1/2×4×3=1/2×3BE+1/2×5BE,
∴BE=3/2.
在Rt△ABD中,BD=AB·sinA=12/5,
∴DF=BD - BF=12/5 - 3/2=9/10.
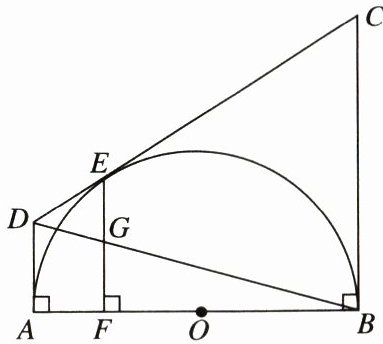
24. (12分)如图,在四边形ABCD中,∠DAB= ∠ABC= 90°,CD与以AB为直径的半圆相切于点E,EF⊥AB于点F,EF交BD于点G,设AD= a,BC= b.
(1)求CD的长度.(用a,b表示)
(2)求EG的长度.(用a,b表示)
(3)试判断EG与FG是否相等,并说明理由.
(1)求CD的长度.(用a,b表示)
(2)求EG的长度.(用a,b表示)
(3)试判断EG与FG是否相等,并说明理由.

答案:
解:
(1)
∵AB为半圆的直径,∠DAB=∠ABC=90°,
∴DA,BC为半圆O的切线.
又
∵CD与以AB为直径的半圆相切于点E,
∴DE=DA=a,CE=CB=b,
∴CD=a+b.
(2)
∵EF⊥AB,
∴EG//BC,
∴△DEG∽△DCB,
∴EG:BC=DE:DC,即EG:b=a:(a+b),
∴EG=ab/(a+b).
(3)EG与FG相等.理由如下:
∵EG//BC,
∴△DEG∽△DCB,
∴DG/DB=EG/BC,即EG/b=DG/DB①.
又
∵GF//AD,
∴△BFG∽△BAD,
∴FG/AD=BG/BD,即FG/a=BG/BD②.
由①+②得EG/b+FG/a=DG/BD+BG/BD=1.
而EG=ab/(a+b),
∴a/(a+b)+FG/a=1,
∴FG=ab/(a+b),
∴EG=FG.
(1)
∵AB为半圆的直径,∠DAB=∠ABC=90°,
∴DA,BC为半圆O的切线.
又
∵CD与以AB为直径的半圆相切于点E,
∴DE=DA=a,CE=CB=b,
∴CD=a+b.
(2)
∵EF⊥AB,
∴EG//BC,
∴△DEG∽△DCB,
∴EG:BC=DE:DC,即EG:b=a:(a+b),
∴EG=ab/(a+b).
(3)EG与FG相等.理由如下:
∵EG//BC,
∴△DEG∽△DCB,
∴DG/DB=EG/BC,即EG/b=DG/DB①.
又
∵GF//AD,
∴△BFG∽△BAD,
∴FG/AD=BG/BD,即FG/a=BG/BD②.
由①+②得EG/b+FG/a=DG/BD+BG/BD=1.
而EG=ab/(a+b),
∴a/(a+b)+FG/a=1,
∴FG=ab/(a+b),
∴EG=FG.
查看更多完整答案,请扫码查看


