《2025年精彩三年就练这一本九年级数学全一册浙教版》

11. 二次函数$y= x^2-2x+3$的一次项系数是______。

答案： -2

12. 已知点$A(2,5)$,$B(4,5)是抛物线y= 2x^2+bx+c$上的两点,则这条抛物线的对称轴为直线______。

答案： $x = 3$

13. 自由下落的物体的高度$h(m)与下落时间t(s)的关系为h= 4.9t^2$。现有一铁球从离地面$19.6m$高的建筑物顶部做自由下落,到达地面需要的时间是______$s$。

答案： 2

14. 如图,这是二次函数$y= -x^2+2x$的图象,若方程$-x^2+2x= n$有实数解,则$n$的取值范围是______。

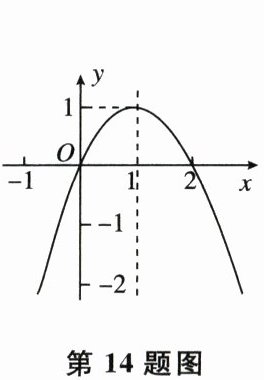
答案： $n≤1$

15. 已知二次函数$y= ax^2+bx+c(a≠0,a,b,c$为常数)的图象,如图所示。下列四个结论：①$b＞0$；②$b＜a+c$；③$c＜4b$；④$a+b＜k^2a+kb$($k$为常数,且$k≠1$)。其中正确结论的序号是______。

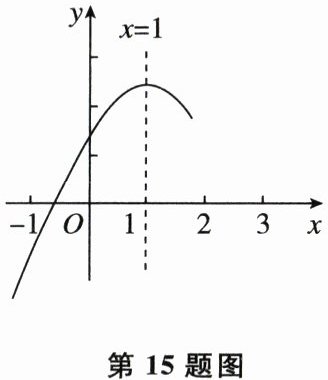
答案： ①③【解析】由图象可知，$a ＜ 0$，$-\frac{b}{2a}=1$，$\therefore b = - 2a$，$\therefore b ＞ 0$，故①正确；由图象可知，当$x = - 1$时，$y ＜ 0$，即$a - b + c ＜ 0$，$\therefore b ＞ a + c$，故②错误；
∵二次函数$y = ax^{2}+bx + c$图象的对称轴为直线$x = 1$，
∴当$x = 3$时，$y = 9a + 3b + c ＜ 0$。又$b = - 2a$，即$a = -\frac{b}{2}$，代入得$9(-\frac{b}{2})+3b + c ＜ 0$，得$c ＜ \frac{3}{2}b$。$\because b ＞ 0$，$\therefore c ＜ 4b$，故③正确；当$x = 1$时，$y$的值最大，此时$y = a + b + c$，而当$x = k$时，$y = ak^{2}+bk + c$。
∵$k$为常数，且$k≠1$，$\therefore a + b + c ＞ ak^{2}+bk + c$，故$a + b ＞ ak^{2}+bk$，故④错误。故①③正确。

16. 若实数$a,b满足a^2+b^2-2a= 0$,则$4a+b^2$的最大值为______。

答案： 8【解析】设$y = 4a + b^{2}$，则$b^{2}=y - 4a$。$\because a^{2}+b^{2}-2a = 0$，$\therefore a^{2}+y - 4a - 2a = 0$，$\therefore y = - a^{2}+6a = - (a^{2}-6a + 9 - 9)= - (a - 3)^{2}+9$。$\because b^{2}=y - 4a$，$\therefore y - 4a≥0$，即$- a^{2}+6a - 4a = - a^{2}+2a≥0$，$\therefore 0≤a≤2$。$\because$当$a ＜ 3$时，$y$随$a$的增大而增大，
∴当$a = 2$时，$y$有最大值，即$4a + b^{2}$有最大值，最大值为8。

17. (8分)已知二次函数$y= -\frac{1}{2}x^2$,解答下列问题：
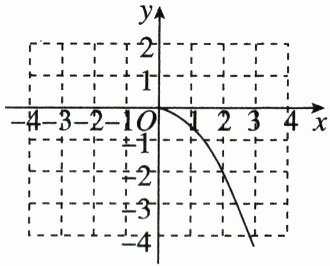
(1)根据已知的图象部分,画出这个函数图象的另一部分。(直接在网格中作图即可)
(2)判断点$(-2,4)$是否在这个函数图象上,说明理由。
(3)求当$y= -4$时对应的函数图象上的点的坐标。

答案：
解：
(1)由已知的图象部分，画出这个函数图象的另一部分，如图。
(2)把点$(-2,4)$的坐标代入$y = -\frac{1}{2}x^{2}$，则$4≠-\frac{1}{2}×(-2)^{2}$，故点$(-2,4)$不在这个函数图象上。
(3)当$y = - 4$时，则$-\frac{1}{2}x^{2}=-4$，解得$x = ±2\sqrt{2}$，
∴当$y = - 4$时对应的函数图象上的点的坐标为$(-2\sqrt{2},-4)$和$(2\sqrt{2},-4)$。

18. (8分)求下列二次函数的最大值或最小值：
(1)$y= 2x^2+3x-4$。
(2)$y= -x^2+4x$。

答案： 解：
(1)$\because y = 2x^{2}+3x - 4 = 2(x + \frac{3}{4})^{2}-\frac{41}{8}$，
∴二次函数的图象开口向上，有最小值，最小值为$-\frac{41}{8}$。
(2)$\because y = - x^{2}+4x = - (x - 2)^{2}+4$，
∴二次函数的图象开口向下，有最大值，最大值为4。