10. 在$\triangle ABC$中,$\angle A,\angle C$是锐角,若$AB= 2$,且$\tan C= 2\tan A$,则$\triangle ABC$面积的最大值是( )
A.$\frac{3}{2}$
B.$4\sqrt{2}$
C.6
D.8
A.$\frac{3}{2}$
B.$4\sqrt{2}$
C.6
D.8
答案:
A [解析]如图,过B作BD⊥AC于D.
∵tanC=$\frac{BD}{CD}$,tanA=$\frac{BD}{AD}$,tanC=2tanA,
∴AD=2CD.
设BD=h,CD=a,则AD=2a.
在Rt△ABD中,h²+4a²=4,
∴h²=4 - 4a².
∵a²h²=a²(4 - 4a²)=4a² - 4a⁴=4[$\frac{1}{4}$ - (a² - $\frac{1}{2}$)²],
当a²=$\frac{1}{2}$时,a²h²取最大值,为1,
∴a²h²≤1,
∴0<ah≤1.
∵S△ABC=$\frac{1}{2}$AC·BD=$\frac{1}{2}$·3a·h=$\frac{3}{2}$ah,
∴$\frac{3}{2}$ah≤$\frac{3}{2}$×1=$\frac{3}{2}$,
∴△ABC面积的最大值是$\frac{3}{2}$.

A [解析]如图,过B作BD⊥AC于D.
∵tanC=$\frac{BD}{CD}$,tanA=$\frac{BD}{AD}$,tanC=2tanA,
∴AD=2CD.
设BD=h,CD=a,则AD=2a.
在Rt△ABD中,h²+4a²=4,
∴h²=4 - 4a².
∵a²h²=a²(4 - 4a²)=4a² - 4a⁴=4[$\frac{1}{4}$ - (a² - $\frac{1}{2}$)²],
当a²=$\frac{1}{2}$时,a²h²取最大值,为1,
∴a²h²≤1,
∴0<ah≤1.
∵S△ABC=$\frac{1}{2}$AC·BD=$\frac{1}{2}$·3a·h=$\frac{3}{2}$ah,
∴$\frac{3}{2}$ah≤$\frac{3}{2}$×1=$\frac{3}{2}$,
∴△ABC面积的最大值是$\frac{3}{2}$.

11. 已知在锐角三角形$ABC$中,$\tan A= \frac{\sqrt{3}}{3}$,则$\angle A$的度数是______.
答案:
30°
12. 在$Rt\triangle ABC$中,$\angle C= 90^{\circ},AB= 3BC$,则$\cos B= $______.
答案:
$\frac{1}{3}$
13. 如图,$\triangle ABC$的顶点都在方格纸的格点上,则$\cos A= $______.


答案:
$\frac{2\sqrt{5}}{5}$
14. 如图,在$\triangle ABC$中,$BC= \sqrt{6}+\sqrt{2},\angle C= 45^{\circ},AB= \sqrt{2}AC$,则$AC$的长为______.


答案:
2
15. 在$\triangle ABC$中,$\angle C= 90^{\circ},\angle A= 30^{\circ}$,直角边$AC的中点为D$,点$E在斜边上且AE= 3$.若$\triangle ADE$为直角三角形,则$BC$的值为______.
答案:
3或4
16. 已知在$\triangle ABC$中,$\angle A= 45^{\circ},AB= 4\sqrt{2},BC= \sqrt{17}$,则$AC= $______.
答案:
5或3 [解析]过B作BH⊥AC于H.
①当H在边AC上时,如图1.
∵∠A=45°,BH⊥AC,
∴△ABH是等腰直角三角形,
∴AH=BH=$\frac{AB}{\sqrt{2}}$=4.
在Rt△BHC中,
CH=$\sqrt{BC² - BH²}$=$\sqrt{(\sqrt{17})² - 4²}$=1.
∴AC=AH + CH=4 + 1=5.

②当H在边AC的延长线上时,如图2.
同理可得AH=BH=4,CH=1,
∴AC=AH - CH=3.
综上所述,AC的长为5或3.

5或3 [解析]过B作BH⊥AC于H.
①当H在边AC上时,如图1.
∵∠A=45°,BH⊥AC,
∴△ABH是等腰直角三角形,
∴AH=BH=$\frac{AB}{\sqrt{2}}$=4.
在Rt△BHC中,
CH=$\sqrt{BC² - BH²}$=$\sqrt{(\sqrt{17})² - 4²}$=1.
∴AC=AH + CH=4 + 1=5.

②当H在边AC的延长线上时,如图2.
同理可得AH=BH=4,CH=1,
∴AC=AH - CH=3.
综上所述,AC的长为5或3.

17. (8分)在$Rt\triangle ABC$中,$\angle C= 90^{\circ},a,b,c分别是\angle A,\angle B,\angle C$的对边.
(1)已知$c= 2\sqrt{3},b= \sqrt{6}$,求$\angle A$.
(2)已知$c= 12,\sin A= \frac{1}{2}$,求$b$.
(1)已知$c= 2\sqrt{3},b= \sqrt{6}$,求$\angle A$.
(2)已知$c= 12,\sin A= \frac{1}{2}$,求$b$.
答案:
解:
(1)
∵cosA=$\frac{b}{c}$=$\frac{\sqrt{6}}{2\sqrt{3}}$=$\frac{\sqrt{2}}{2}$,
∴∠A=45°.
(2)
∵sinA=$\frac{1}{2}$=$\frac{a}{c}$=$\frac{a}{12}$,
∴a=6,
∴b=$\sqrt{c² - a²}$=6$\sqrt{3}$
(1)
∵cosA=$\frac{b}{c}$=$\frac{\sqrt{6}}{2\sqrt{3}}$=$\frac{\sqrt{2}}{2}$,
∴∠A=45°.
(2)
∵sinA=$\frac{1}{2}$=$\frac{a}{c}$=$\frac{a}{12}$,
∴a=6,
∴b=$\sqrt{c² - a²}$=6$\sqrt{3}$
18. (8分)计算:
(1)$\tan 45^{\circ}-\sin 30^{\circ}\cos 60^{\circ}-\cos^{2}45^{\circ}$.
(2)$3\tan 30^{\circ}-\tan^{2}45^{\circ}+2\sin 60^{\circ}$.
(1)$\tan 45^{\circ}-\sin 30^{\circ}\cos 60^{\circ}-\cos^{2}45^{\circ}$.
(2)$3\tan 30^{\circ}-\tan^{2}45^{\circ}+2\sin 60^{\circ}$.
答案:
解:
(1)tan45° - sin30°cos60° - cos²45°
=1 - $\frac{1}{2}$×$\frac{1}{2}$ - ($\frac{\sqrt{2}}{2}$)²=1 - $\frac{1}{4}$ - $\frac{1}{2}$=$\frac{1}{4}$.
(2)3tan30° - tan²45° + 2sin60°
=3×$\frac{\sqrt{3}}{3}$ - 1² + 2×$\frac{\sqrt{3}}{2}$=$\sqrt{3}$ - 1 + $\sqrt{3}$=2$\sqrt{3}$ - 1.
(1)tan45° - sin30°cos60° - cos²45°
=1 - $\frac{1}{2}$×$\frac{1}{2}$ - ($\frac{\sqrt{2}}{2}$)²=1 - $\frac{1}{4}$ - $\frac{1}{2}$=$\frac{1}{4}$.
(2)3tan30° - tan²45° + 2sin60°
=3×$\frac{\sqrt{3}}{3}$ - 1² + 2×$\frac{\sqrt{3}}{2}$=$\sqrt{3}$ - 1 + $\sqrt{3}$=2$\sqrt{3}$ - 1.
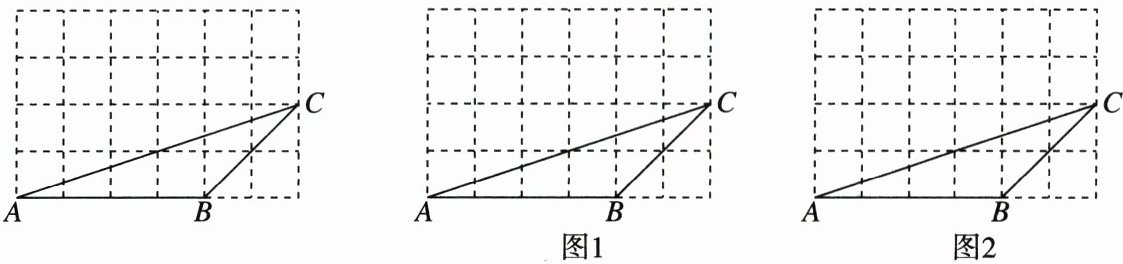
19. (8分)如图,在$4×6$的网格中,$\triangle ABC$的顶点都在边长为1的小正方形的顶点上.
(1)$\angle CAB$的正切值为______.
(2)分别在图1和图2中各画一个格点三角形,使得所画的三角形和$\triangle ABC$相似且不全等.(所画的两个三角形也不全等)
(1)$\angle CAB$的正切值为______.
(2)分别在图1和图2中各画一个格点三角形,使得所画的三角形和$\triangle ABC$相似且不全等.(所画的两个三角形也不全等)

答案:
(1)$\frac{1}{3}$
(2)如图1和图2,△A'B'C'即为所求.


(1)$\frac{1}{3}$
(2)如图1和图2,△A'B'C'即为所求.


查看更多完整答案,请扫码查看


