23. (10分)(1)如图1,AD是△ABC的中线,点E是AB边上一点,作EF//BC交AC于F,交AD于G.证
明:AD平分EF.
(2)如图2,AD是△ABC的中线,点M是AD的中点,连结BM并延长与AC交于点N,,求$\frac{AN}{NC}$的值.
(3)如图3,若$\frac{BD}{BC}$= $\frac{1}{m}$,$\frac{AE}{AD}$= $\frac{1}{n}$(m>1,n>1),直接写出$\frac{AF}{AC}$的值.

明:AD平分EF.
(2)如图2,AD是△ABC的中线,点M是AD的中点,连结BM并延长与AC交于点N,,求$\frac{AN}{NC}$的值.
(3)如图3,若$\frac{BD}{BC}$= $\frac{1}{m}$,$\frac{AE}{AD}$= $\frac{1}{n}$(m>1,n>1),直接写出$\frac{AF}{AC}$的值.

答案:
解:
(1)证明:
∵AD是△ABC的中线,
∴BD=CD.
∵EF//BC交AC于F,交AD于G,
∴△AEG∽△ABD,△AFG∽△ACD,
∴$\frac{EG}{BD}=\frac{AG}{AD}$,$\frac{FG}{CD}=\frac{AG}{AD}$,
∴$\frac{EG}{BD}=\frac{FG}{CD}$,
∴$\frac{EG}{FG}=\frac{BD}{CD}=1$,
∴EG=FG,
∴AD平分EF.
(2)如图1,作DG//BN交AC于点G.
∵AD是△ABC的中线,点M是AD的中点,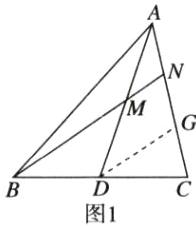
∴BD=CD,AM=MD,
∴$\frac{CG}{NG}=\frac{CD}{BD}=1$,$\frac{AN}{NG}=\frac{AM}{MD}=1$,
∴CG=NG,AN=NG,
∴AN=NG=CG,NC=NG + CG=2AN,
∴$\frac{AN}{NC}=\frac{1}{2}$.
(3)$\frac{AF}{AC}$的值是$\frac{1}{mn - m + 1}$.如图2,作DH//BF交AC于点H.
∵$\frac{BD}{BC}=\frac{1}{m}$,
∴$\frac{FH}{FC}=\frac{BD}{BC}=\frac{1}{m}$,
∴FC=mFH.
∵EF//DH,$\frac{AE}{AD}=\frac{1}{n}$,
∴$\frac{AF}{AH}=\frac{AE}{AD}=\frac{1}{n}$,
∴AH=nAF,
∴AF + FH=nAF,
∴$AF=\frac{1}{n - 1}FH$,
∴$AC=FC + AF=mFH+\frac{1}{n - 1}FH=\frac{mn - m + 1}{n - 1}FH$,
∴$\frac{AF}{AC}=\frac{\frac{1}{n - 1}FH}{\frac{mn - m + 1}{n - 1}FH}=\frac{1}{mn - m + 1}$,
∴$\frac{AF}{AC}$的值是$\frac{1}{mn - m + 1}$.
解:
(1)证明:
∵AD是△ABC的中线,
∴BD=CD.
∵EF//BC交AC于F,交AD于G,
∴△AEG∽△ABD,△AFG∽△ACD,
∴$\frac{EG}{BD}=\frac{AG}{AD}$,$\frac{FG}{CD}=\frac{AG}{AD}$,
∴$\frac{EG}{BD}=\frac{FG}{CD}$,
∴$\frac{EG}{FG}=\frac{BD}{CD}=1$,
∴EG=FG,
∴AD平分EF.
(2)如图1,作DG//BN交AC于点G.
∵AD是△ABC的中线,点M是AD的中点,

∴BD=CD,AM=MD,
∴$\frac{CG}{NG}=\frac{CD}{BD}=1$,$\frac{AN}{NG}=\frac{AM}{MD}=1$,
∴CG=NG,AN=NG,
∴AN=NG=CG,NC=NG + CG=2AN,
∴$\frac{AN}{NC}=\frac{1}{2}$.
(3)$\frac{AF}{AC}$的值是$\frac{1}{mn - m + 1}$.如图2,作DH//BF交AC于点H.
∵$\frac{BD}{BC}=\frac{1}{m}$,
∴$\frac{FH}{FC}=\frac{BD}{BC}=\frac{1}{m}$,
∴FC=mFH.
∵EF//DH,$\frac{AE}{AD}=\frac{1}{n}$,
∴$\frac{AF}{AH}=\frac{AE}{AD}=\frac{1}{n}$,
∴AH=nAF,
∴AF + FH=nAF,
∴$AF=\frac{1}{n - 1}FH$,
∴$AC=FC + AF=mFH+\frac{1}{n - 1}FH=\frac{mn - m + 1}{n - 1}FH$,
∴$\frac{AF}{AC}=\frac{\frac{1}{n - 1}FH}{\frac{mn - m + 1}{n - 1}FH}=\frac{1}{mn - m + 1}$,
∴$\frac{AF}{AC}$的值是$\frac{1}{mn - m + 1}$.

24. (12分)在△ABC中,AB= AC,D为BC的中点,以D为顶点作∠MDN= ∠B.

(1)如图1,当射线DN经过点A时,DM交AC边于点E,不添加辅助线,写出图中所有与△ADE相似
的三角形.
(2)如图2,将∠MDN绕点D沿逆时针方向旋转,DM,DN分别交线段AC,AB于点E,F(点E与点A
不重合),不添加辅助线,写出图中所有的相似三角形,并证明你的结论.
(3)在图2中,若AB= AC= 10,BC= 12,当△DEF的面积等于△ABC面积的$\frac{1}{4}$时,求线段EF的长.

(1)如图1,当射线DN经过点A时,DM交AC边于点E,不添加辅助线,写出图中所有与△ADE相似
的三角形.
(2)如图2,将∠MDN绕点D沿逆时针方向旋转,DM,DN分别交线段AC,AB于点E,F(点E与点A
不重合),不添加辅助线,写出图中所有的相似三角形,并证明你的结论.
(3)在图2中,若AB= AC= 10,BC= 12,当△DEF的面积等于△ABC面积的$\frac{1}{4}$时,求线段EF的长.
答案:
解:
(1)与△ADE相似的三角形有△ABD,△ACD,△DCE.证明:
∵AB=AC,D为BC的中点,
∴AD⊥BC,∠B=∠C,∠BAD=∠CAD.又
∵∠MDN=∠B,
∴△ADE∽△ABD.同理可得,△ADE∽△ACD.
∵∠B + ∠BAD=90°,∠ADE + ∠EDC=90°,∠B=∠MDN,
∴∠BAD=∠EDC.
∵∠B=∠C,
∴△ABD∽△DCE,
∴△ADE∽△DCE.
(2)△BDF∽△CED∽△DEF.证明:
∵∠B + ∠BDF + ∠BFD=180°,∠EDF + ∠BDF + ∠CDE=180°,又
∵∠EDF=∠B,
∴∠BFD=∠CDE.由AB=AC,得∠B=∠C,
∴△BDF∽△CED,
∴$\frac{BD}{DF}=\frac{EC}{DE}$.
∵BD=CD,
∴$\frac{CD}{DF}=\frac{EC}{DE}$.又
∵∠C=∠EDF,
∴△CED∽△DEF,
∴△BDF∽△CED∽△DEF.
(3)如图,连结AD,过点D作DG⊥EF,DH⊥BF,垂足分别为G,H.
∵AB=AC,D是BC的中点,
∴AD⊥BC,$BD=\frac{1}{2}BC=6$. 在Rt△ABD中,$AD^2=AB^2 - BD^2$,
在Rt△ABD中,$AD^2=AB^2 - BD^2$,
∴AD=8,
∴$S_{\triangle ABC}=\frac{1}{2}BC\cdot AD=\frac{1}{2}×12×8=48$,$S_{\triangle DEF}=\frac{1}{4}S_{\triangle ABC}=\frac{1}{4}×48=12$.又
∵$\frac{1}{2}AD\cdot BD=\frac{1}{2}AB\cdot DH$,
∴$DH=\frac{AD\cdot BD}{AB}=\frac{8×6}{10}=\frac{24}{5}$.由
(2)知,△BDF∽△DEF,
∴∠DFB=∠EFD.
∵DG⊥EF,DH⊥BF,
∴$DH=DG=\frac{24}{5}$.
∵$S_{\triangle DEF}=\frac{1}{2}EF\cdot DG=12$,
∴$EF=\frac{12}{\frac{1}{2}DG}=5$.
解:
(1)与△ADE相似的三角形有△ABD,△ACD,△DCE.证明:
∵AB=AC,D为BC的中点,
∴AD⊥BC,∠B=∠C,∠BAD=∠CAD.又
∵∠MDN=∠B,
∴△ADE∽△ABD.同理可得,△ADE∽△ACD.
∵∠B + ∠BAD=90°,∠ADE + ∠EDC=90°,∠B=∠MDN,
∴∠BAD=∠EDC.
∵∠B=∠C,
∴△ABD∽△DCE,
∴△ADE∽△DCE.
(2)△BDF∽△CED∽△DEF.证明:
∵∠B + ∠BDF + ∠BFD=180°,∠EDF + ∠BDF + ∠CDE=180°,又
∵∠EDF=∠B,
∴∠BFD=∠CDE.由AB=AC,得∠B=∠C,
∴△BDF∽△CED,
∴$\frac{BD}{DF}=\frac{EC}{DE}$.
∵BD=CD,
∴$\frac{CD}{DF}=\frac{EC}{DE}$.又
∵∠C=∠EDF,
∴△CED∽△DEF,
∴△BDF∽△CED∽△DEF.
(3)如图,连结AD,过点D作DG⊥EF,DH⊥BF,垂足分别为G,H.
∵AB=AC,D是BC的中点,
∴AD⊥BC,$BD=\frac{1}{2}BC=6$.
 在Rt△ABD中,$AD^2=AB^2 - BD^2$,
在Rt△ABD中,$AD^2=AB^2 - BD^2$,∴AD=8,
∴$S_{\triangle ABC}=\frac{1}{2}BC\cdot AD=\frac{1}{2}×12×8=48$,$S_{\triangle DEF}=\frac{1}{4}S_{\triangle ABC}=\frac{1}{4}×48=12$.又
∵$\frac{1}{2}AD\cdot BD=\frac{1}{2}AB\cdot DH$,
∴$DH=\frac{AD\cdot BD}{AB}=\frac{8×6}{10}=\frac{24}{5}$.由
(2)知,△BDF∽△DEF,
∴∠DFB=∠EFD.
∵DG⊥EF,DH⊥BF,
∴$DH=DG=\frac{24}{5}$.
∵$S_{\triangle DEF}=\frac{1}{2}EF\cdot DG=12$,
∴$EF=\frac{12}{\frac{1}{2}DG}=5$.
查看更多完整答案,请扫码查看


